阐述一些底层的卷积实现方式：包含：滑动窗口、im2col + gemm、winograd 等

卷积的具体实现有如下几种方法：

• 直接卷积 direct：按照定义直接计算， 一般来说，访存很差。在特定情况下可能是最优方案。
• im2col+gemm：先将特征图换成矩阵，然后用kernel矩阵乘以特征图转换的矩阵，得到输出，访存性能能好一些
• winograd：用加法换乘法，通过减少乘法次数来提高卷积执行速度。

此外还有 Strassen(减少卷积操作数) 和 FFT(通过 FFT 来减少 conv 的计算量、在大卷积核下收益明显) 、MEC 等方法。但是这几种方案并非主流。下面我们主要详细来阐述主流的三种方案。

本文主要从工程的角度来阐述这三种主流方案，对于具体的理论推导和细节原理，则不涉及。

一. direct

直接按照定义进行计算。需要进行多重 for 循环的展开。

二. im2col + gemm

Im2col(Image to Column)把输入 feature map 按照卷积核的形式一一展开并拼接成列，接着通过高性能 MatMul（Matrix Multiplication） Kernel 进行矩阵乘，得到输出 feature map。它的本质是把卷积运算转换成矩阵运算。

Pack 优化:

​ 理论上来说， 获得了输入特征图和卷积核的 im2col 变换矩阵之后其实就可以利用 Sgemm 计算出卷积的结果了。

​ 但是如果直接使用矩阵乘法计算，在卷积核尺寸比较大并且输出特征图通道数也比较大的时候，我们会发现这个时候 im2col 获得矩阵是一个行非常多列非常少的矩阵，在做矩阵乘法的时候访存会变得比较差，从而降低计算效率。这里有一个优化技巧，就是数据打包(Pack)。具体来说，对于卷积核我们进行的Pack（所谓 4 的Pack就是在 im2Col获得的二维矩阵的高维度进行压缩，在宽维度进行膨胀，每四行进行交叉拼接）。 如下图所示， 这是一个的卷积核并且输出通道数为，它经过Im2Col之后首先变成上图的上半部分，然后经过Pack 之后变成了上图的下半部分，即变成了每个卷积核的元素按列方向交织排列。

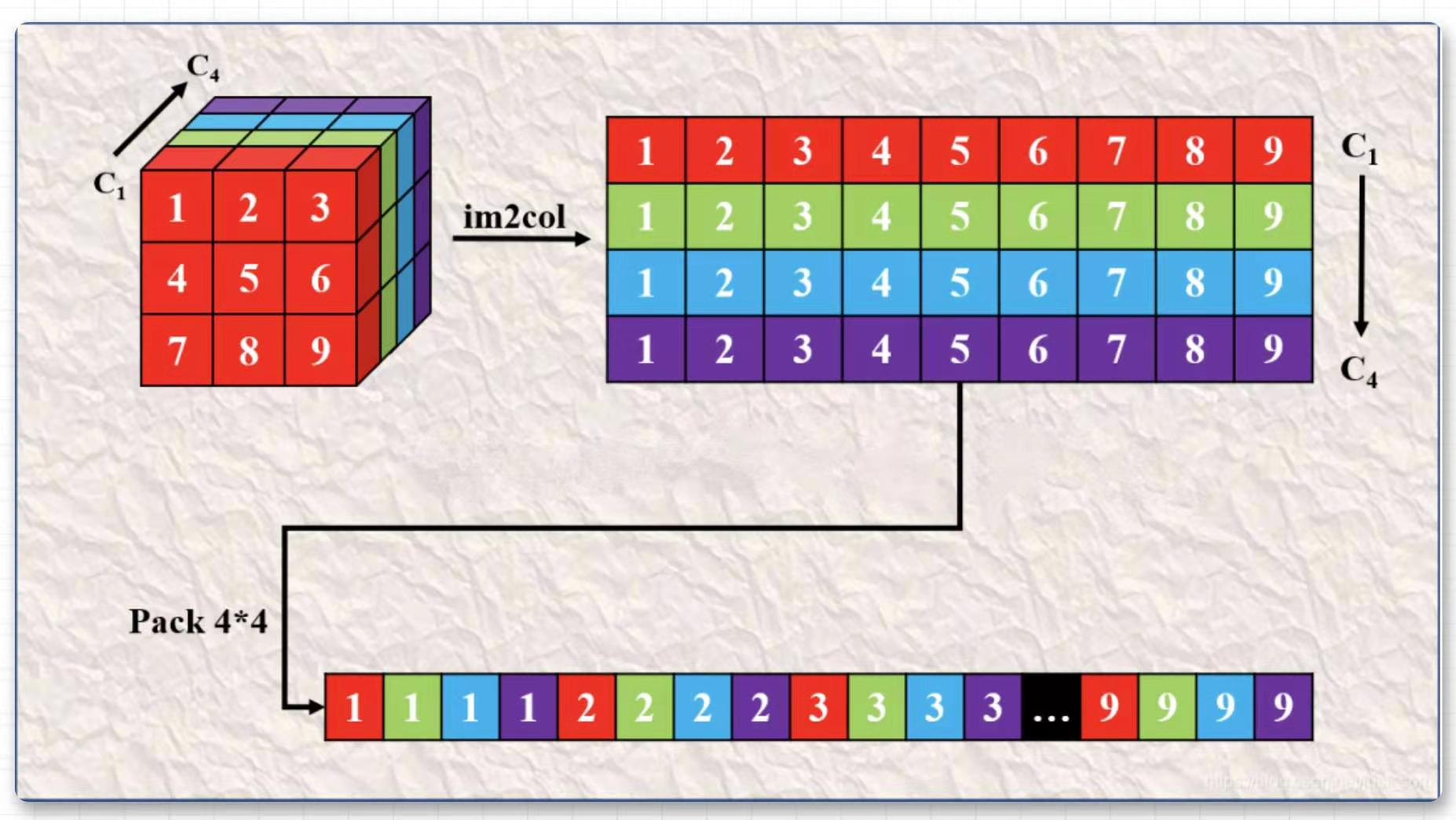
还有一个技巧是，每次在执行卷积计算时，对于 Image 的 Im2col 和 Pack 每次都会执行，但对于卷积核，Im2col 和 Pack 在任意次只用做一次，所以我们可以在模型初始化的时候提前把卷积核给 Pack 好，这样就可以节省卷积核 im2col 和 pack 耗费的时间。

代码实现可以参考： https://github.com/msnh2012/Msnhnet/blob/master/src/layers/arm/MsnhConvolutionSgemm.cpp

三. Winograd

论文参见： https://arxiv.org/abs/1509.09308v2

​ 可以看到 img2col 提高了访存速度，但是它并没有降低运算的时间复杂度。于是在卷积的实践中诞生了 Winograd 算法。Winograd 的 本质是通过降低乘法的次数来提高卷积运算速度。 Winograd 算法主要应用于卷积核为 3x3，步幅为 1 的 2D 卷积神经网络，其参数表示为 F(mxm, rxr)，其中 mxm 是运算之后输出块的大小，rxr 是卷积核的大小，以 F(2x2, 3x3) 和 F(6x6, 3x3) 使用最多，前者加速比可达 2.25x，后者加速比则高达 5.06x。

​ 首先以一维卷积 $F(2,3)$ 为例。设输入信号为

$$d=[d0, d1, d2, d3]^T$$

卷积核为：

$$g=[g0, g1, g2]^T$$

滑动步长为 1，不做 padding 操作，则输出结果可以写成

$$F(2,3)=\left[\begin{array}{ccc}d_0 &d_1 &d_2 \\d_1 &d_2 &d_3\end{array}\right]\left[\begin{array}{ccc}g_0 \\g_1\\g_2\end{array}\right]=\left[\begin{array}{c}r_0\\r_1\end{array}\right]$$

其中

$$r_0=d_0*g_0+d_1*g_1+d_2*g_2 \\ r_1=d_1*g_0+d_2*g_1+d_3*g_2$$

可以看到如果用一般的矩阵乘法，则需要 6 次乘法和 4 次加法。

winograd 做法如下

$$F(2,3)=\left[\begin{array}{ccc}d_0 &d_1 &d_2 \\d_1 &d_2 &d_3\end{array}\right]\left[\begin{array}{ccc}g_0 \\g_1\\g_2\end{array}\right]=\left[\begin{array}{c}m_1+m_2+m_3\\m_2-m_3-m_4\end{array}\right]$$

其中

$$m_1=(d_0-d_2)g_0, \quad m_2=(d_1+d_2)\frac{g_0+g_1+g_2}{2}\\ m_4=(d_1-d_3)g_2, \quad m_3=(d_2-d_1)\frac{g_0-g_1+g_2}{2}\\$$

可以看到利用 winograd 算法需要 4 次乘法，8次加法，相比一般矩阵乘法，通过增加加法运算减少乘法的运算，可以实现加速。

由于 winograd 算法证明比较复杂暂时不写了，直接丢计算公式，一维卷积计算公式如下：

$$Y=A^T\left[[Gg]\bigodot[B^Td]\right]$$

其中 ⨀ 表示 element-wise，A,G,B 都是根据输出大小和卷积核提前确定好的(有人已经写好了,可参考 wincnn)， g 表示卷积核，d 表示输入数据(也就是需要进行卷积计算的数据)。 可以看到，它可以将 $m * r$ 次乘法 降低为 $m + r - 1$ 次乘法。

对应二维卷积计算公式如下:

$$Y=A^T\left[[GgG^T]\bigodot[B^TdB]\right]A$$

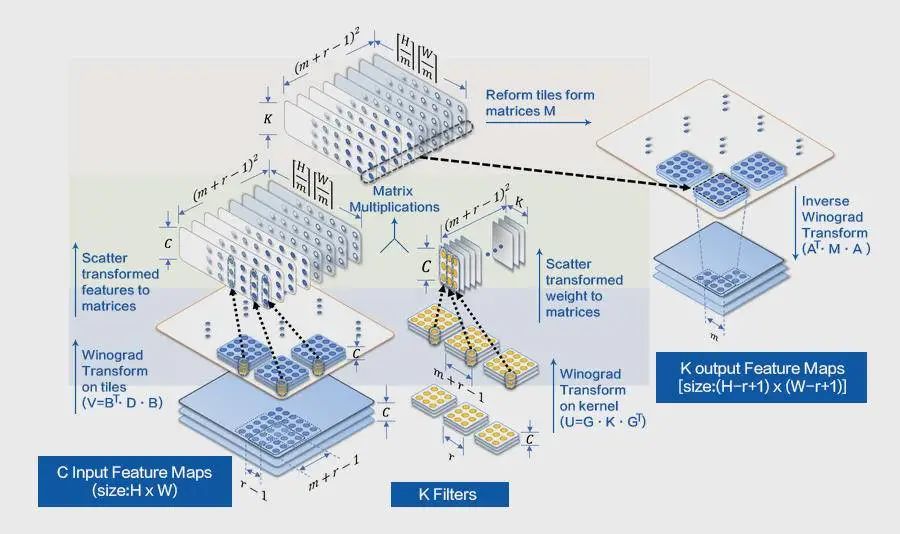
基于上面介绍的二维的 Winograd的原理，我们现在只需要分 4 步即可实现 winograd 算法：

1. 根据卷积核的大小，确定变换矩阵 G， 对输入卷积核的变换 $U = GgG^T$
2. 根据输入数据的大小， 确定变换矩阵 B，并对输入数据的变换 $V = B^T d B$
3. 计算 M 矩阵： $M = \sum U \bigodot V$
4. 计算最终结果: $Y = A^T M A$

需要注意以下几点：

1. 当输入较大的时候， 需要把输入拆成多个 4x4 的 block，stride 2 即可。
2. 当对卷积核和输入数据进行转换后， 需要对其进行内存重拍， 方便去利用 gemm 。

具体的代码实现可以参照： https://github.com/Tencent/ncnn/blob/master/src/layer/arm/convolution_3x3.h line 1702 - line 1864

四. 其他

• 不同的卷积的快慢并非一成不变， 特定的情况下可能通常较快的方法反而运行较快。旷视的 megengine 提出了 Fast-Run 来寻找最优算子，其工程实现分为选择和执行两个阶段：

  • 选择阶段，测速模型每个算子，选出最优实现，保存算子名称和最优实现的映射表；
  • 执行阶段，根据映射表直接调用相应实现完成计算。

• 数据排布和 cache 命中是极其重要的。

• 数据排布(Tensor Layout) ：数据排布是推理侧卷积计算优化方面首先面临的问题。选择合适的数据排布不仅会使卷积优化事半功倍，还可作为其他优化方法的基础， 目前，深度学习框架中常见的数据排布格式有3种：
  • NHWC：[Batch, Height, Width, Channels]
  • NCHW：[Batch, Channels, Height, Width]
  • NCHWX：[Batch, Channels/X, Height, Width, X=4/8]

​ 数据的排布对卷积计算有着整体性的直接影响。NHWC 和 NCHW 的空间复杂度相同，区别在于访存行为，NCHWX 介于两者之间，但是有其他优点。