1. im2col 基本原理

(1) 对于图像的变换：

首先将每个卷积所卷积的区域作为一行，所有的卷积区域纵向排列，作为右乘矩阵。需要注意的是多个通道应该堆叠在下面。如下图所示：

单通道：

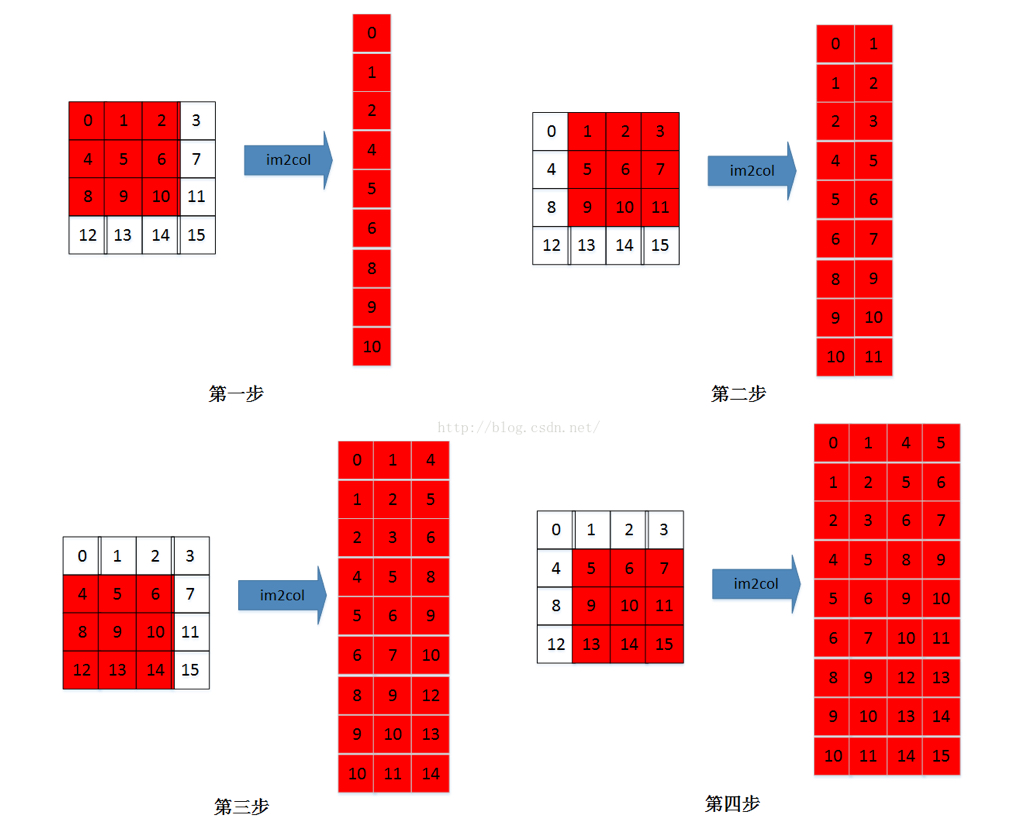
多通道：

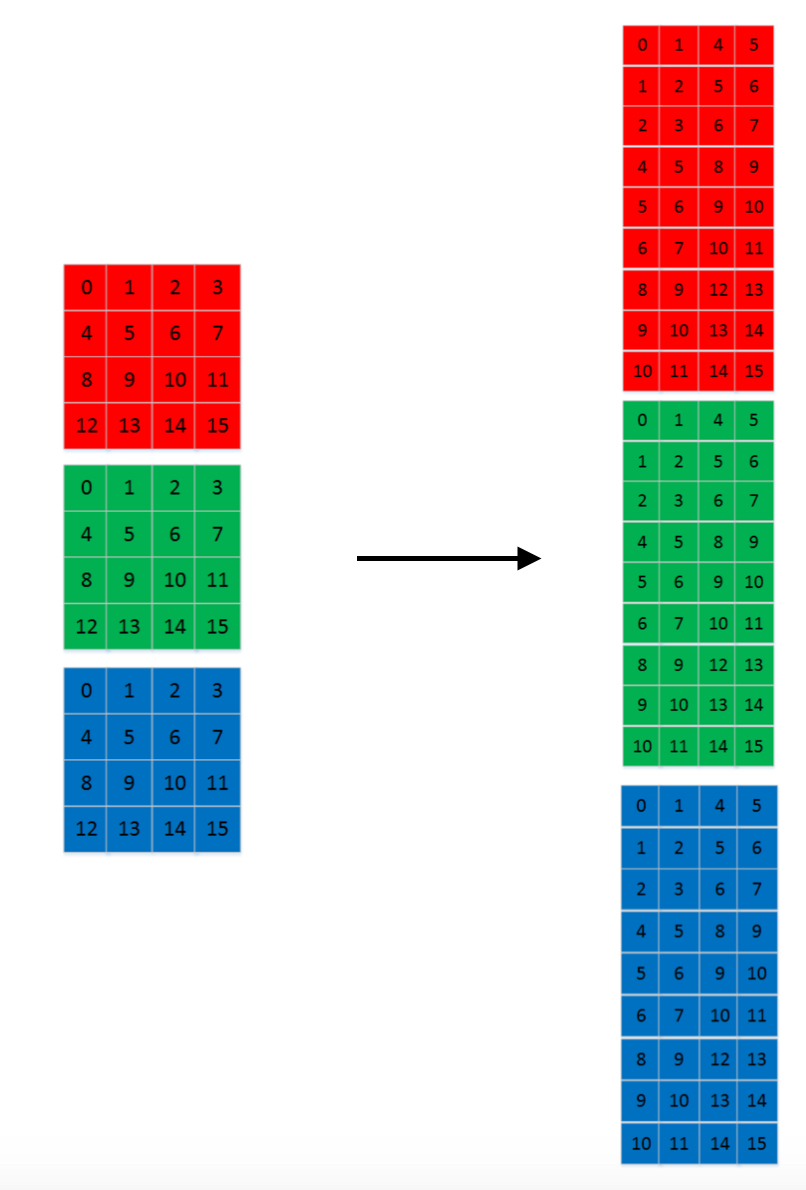
输入特征图转化得到的矩阵尺度 = (卷积组输入通道数*卷积核高*卷积核宽) * (卷积层输出单通道特征图高 * 卷积层输出单通道特征图宽)

(2) 对于卷积核的变换

将一个卷积核拉伸为一个横行，作为左乘矩阵：(为什么要拉伸为横行，在于对应的卷积区域拉伸为竖行，这样才能与之相对应，进行矩阵乘法)

权值矩阵尺度 = (输出层通道数) * (卷积输入通道数*卷积核高*卷积核宽)

(3) 将卷积核矩阵核图像矩阵相乘即可

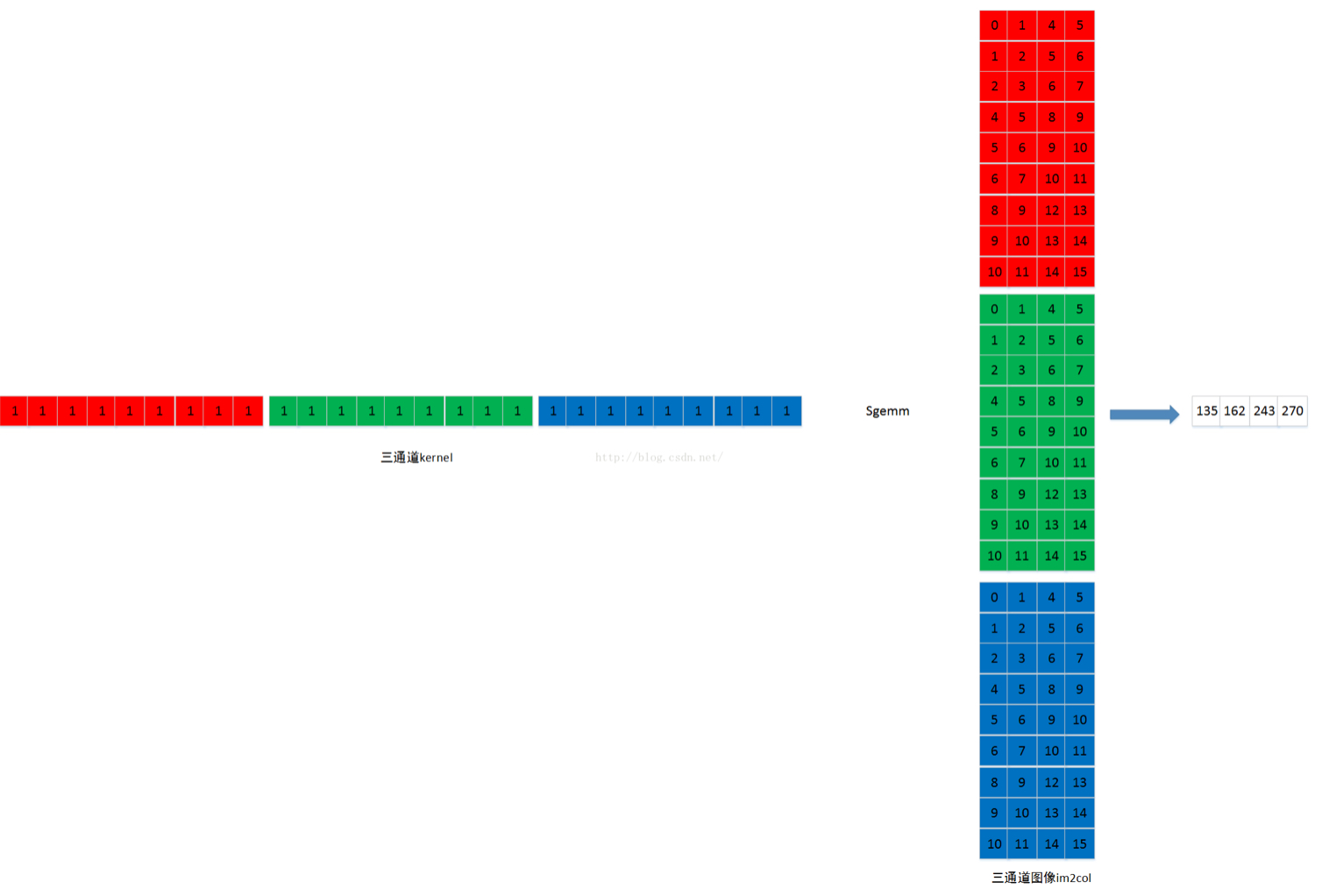
卷积层输出尺度 = (卷积层输出通道数) * (卷积层输出单通道特征图高 * 卷积层输出单通道特征图宽)

最后需要将结果调整成为需要的大小：

(4) 对于多个输出通道图像的卷积

应该纵向堆叠每个卷积层

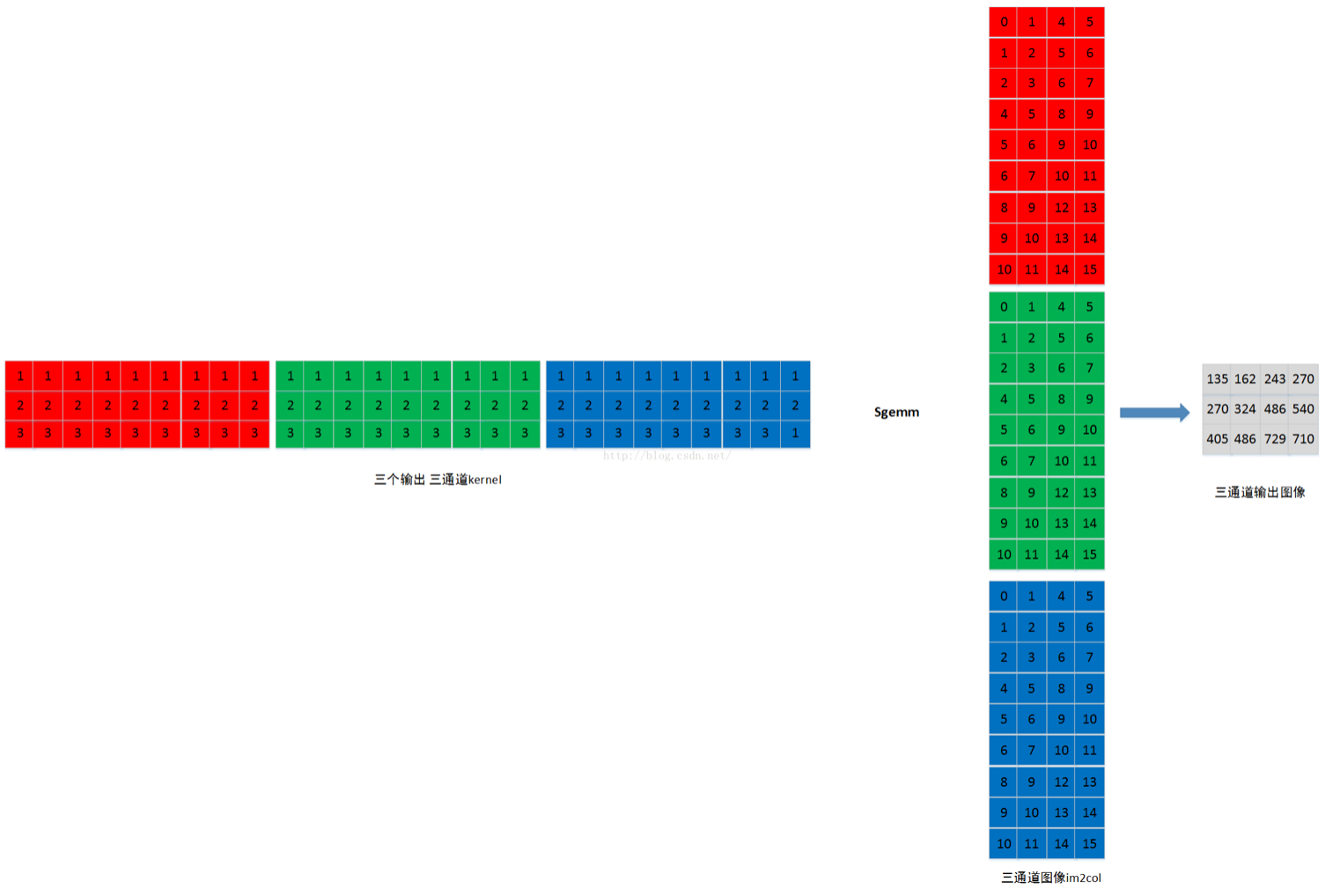
最后再调整输出矩阵：

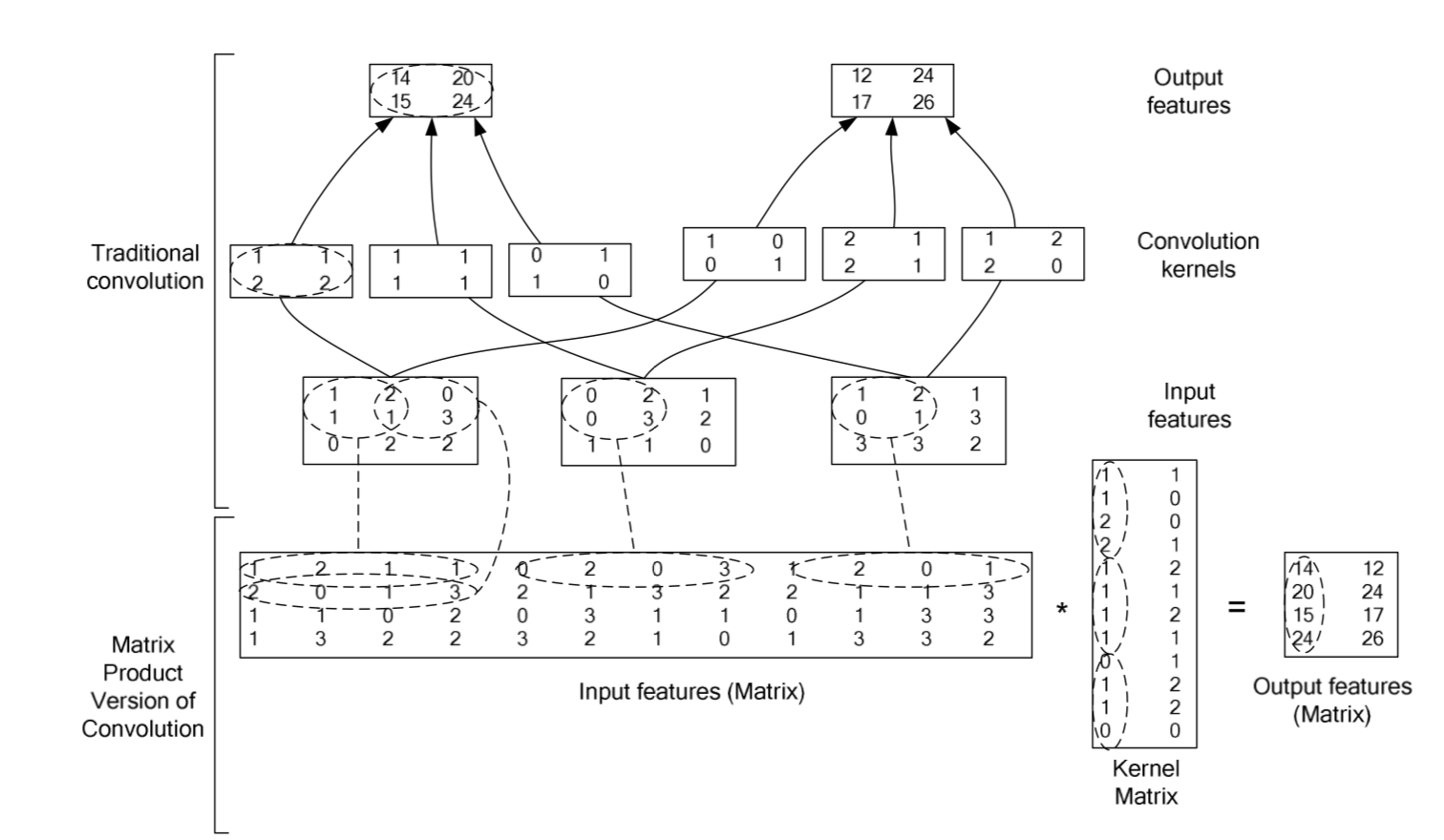
2. 总体简图：

下面是一个整体矩阵乘法的简图：

3. im2col_cpu 源码剖析

im2col_cpu函数将卷积层输入转化为矩阵相乘的右元，核心是5个for循环，首先第一个for循环表示按照输入的通道数逐个处理卷积层输入的特征图，下面笔者将用图示表示剩余的四个for循环操作，向读者朋友们展示卷积层输入的单通道特征图是通过怎样的方式转化为一个矩阵。在这里我们假设，卷积层输入单通道特征图原大小为5*5，高和宽方向的pad为1，高和宽方向步长为2，卷积核不进行扩展。

我们先计算一下，卷积层输入单通道特征图转化得到的矩阵的尺度，矩阵的行数应该为卷积核高卷积核宽，即为9，列数应该为卷积层输出特征图高(output_h)卷积层输出特征图宽(output_w)，也为9，那么，im2col算法起始由下图开始：

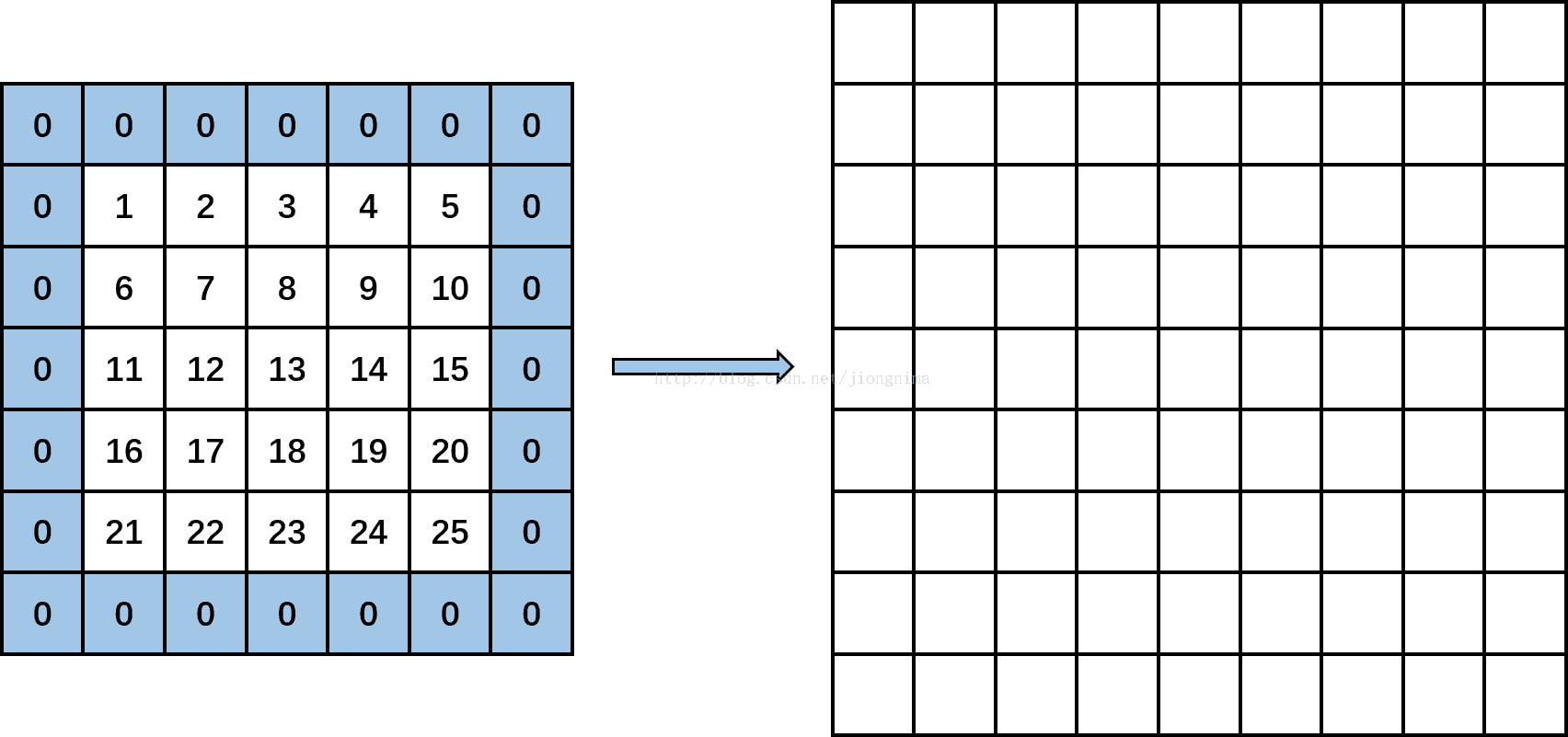
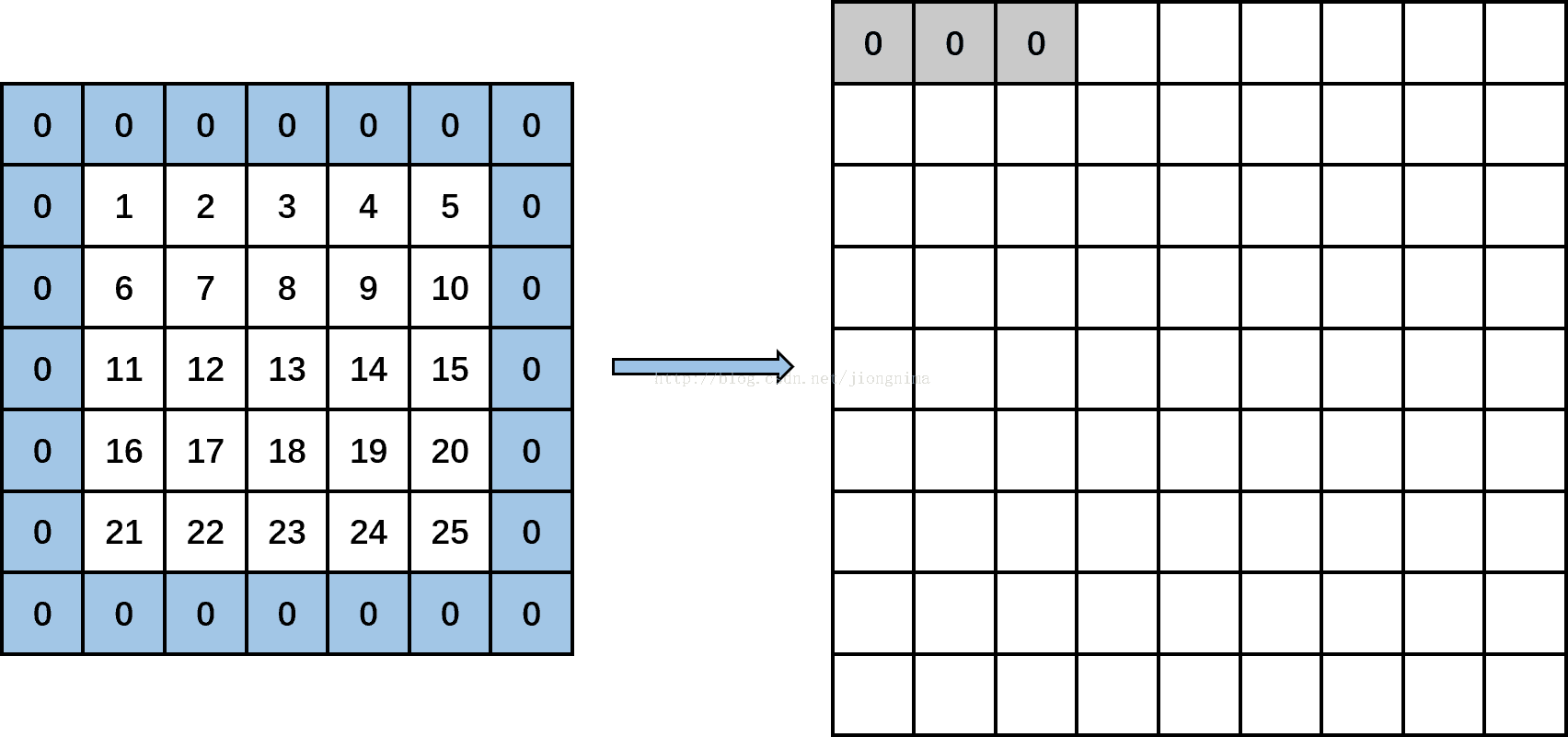
首先kernel_row为0，kernel_col也为0。按照input_row = -pad_h + kernel_row * dilation_h计算input_row的值，在这里，pad_h为1，kernel_row为0，dilation_h为1，计算出input_row为-1，此时output_row为3，满足函数中的第一个if条件，那么在输出图像上先置output_w个零，因为output_w为3，因此得到下图：

然后input_row加上步长2，由-1变成1，此时output_rows为2，计算input_col等于-1，此时执行input_col定义下面的for循环，得到3个值：依次往目标矩阵中填入0，data_im[1*5+1]和data_im[1*5+3]，即填入0,7和9。得到下图：

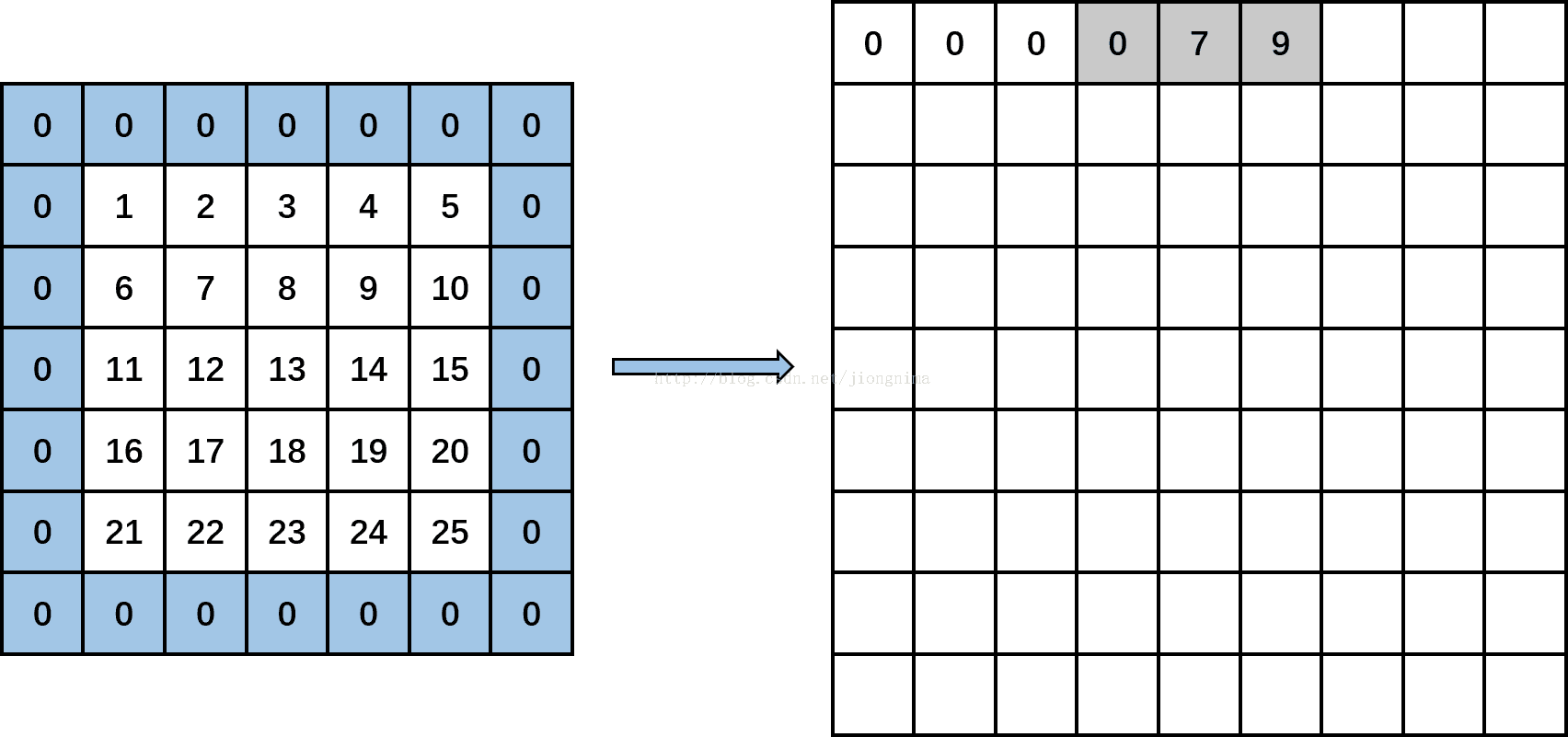
再接着执行，此时input_row再加上2变为3，此时output_rows变为1，计算input_col等于-1，执行input_col定义下面的for循环，得到3个值，分别为0，data_im[3*5+1]和data_im[3*5+3]，即填入0,17和19。得到下图：(以上操作是将第一个通道的卷积对应第一个对应位置进放好)

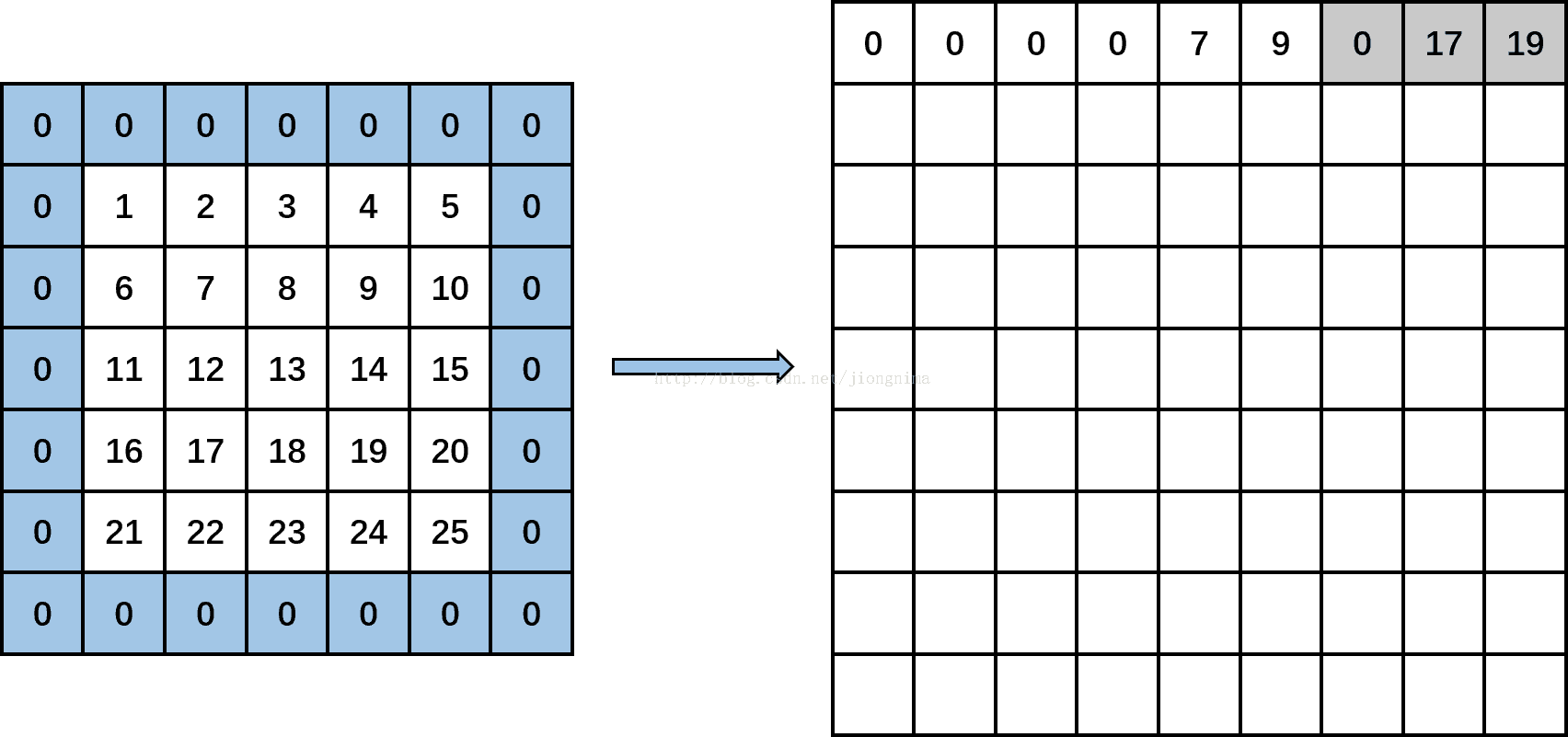
接着，kernel_col变成1，此时kernel_row为0，kernel_col为1。计算input_row又变成-1，第一个if条件成立，那么，再在输出矩阵上输出3个0。然后，input_row变成1，input_col分别为0(-1+1)，2(-1+1+2)和4(-1+1+2+2)时，输出矩阵上分别输出data_im[1*5+0]，data[1*5+2]，data[1*5+4]，即分别填入6,8,10。然后，input_row变成3，input_col分别为0，2，4时，输出矩阵上分别输出data_im[3*5+0]，data[3*5+2]，data[3*5+4]，即分别输出16,18,20。（将第一个通道的卷积对应第二个对应位置进放好）

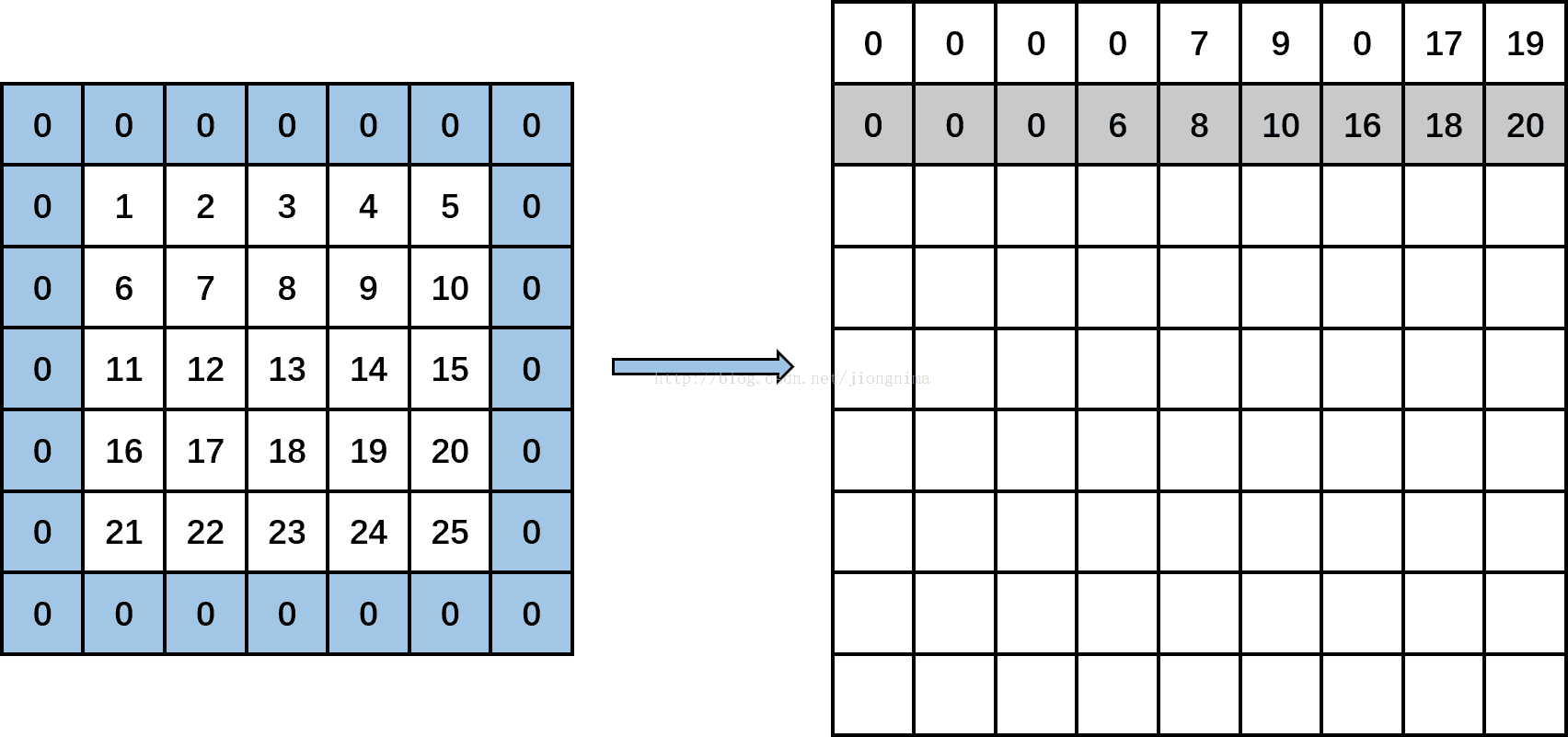
然后，kernel_col变成2，此时kernel_row为0，kernel_col为2。计算input_row又变成-1，第一个if条件成立，那么，再在输出矩阵上输出3个0。然后，input_row变成1，input_col分别为1(-1+2)，3(-1+2+2)和5(-1+2+2+2)时，输出矩阵上分别输出data_im[1*5+1]，data[1*5+3]，0，即分别填入7,9,0。然后，input_row变成3，input_col分别为1，3，5时，输出矩阵上分别输出data_im[3*5+0]，data[3*5+2]，0，即分别输出17,19,0。见下图：（将第一个通道的卷积对应第三个对应位置进放好）

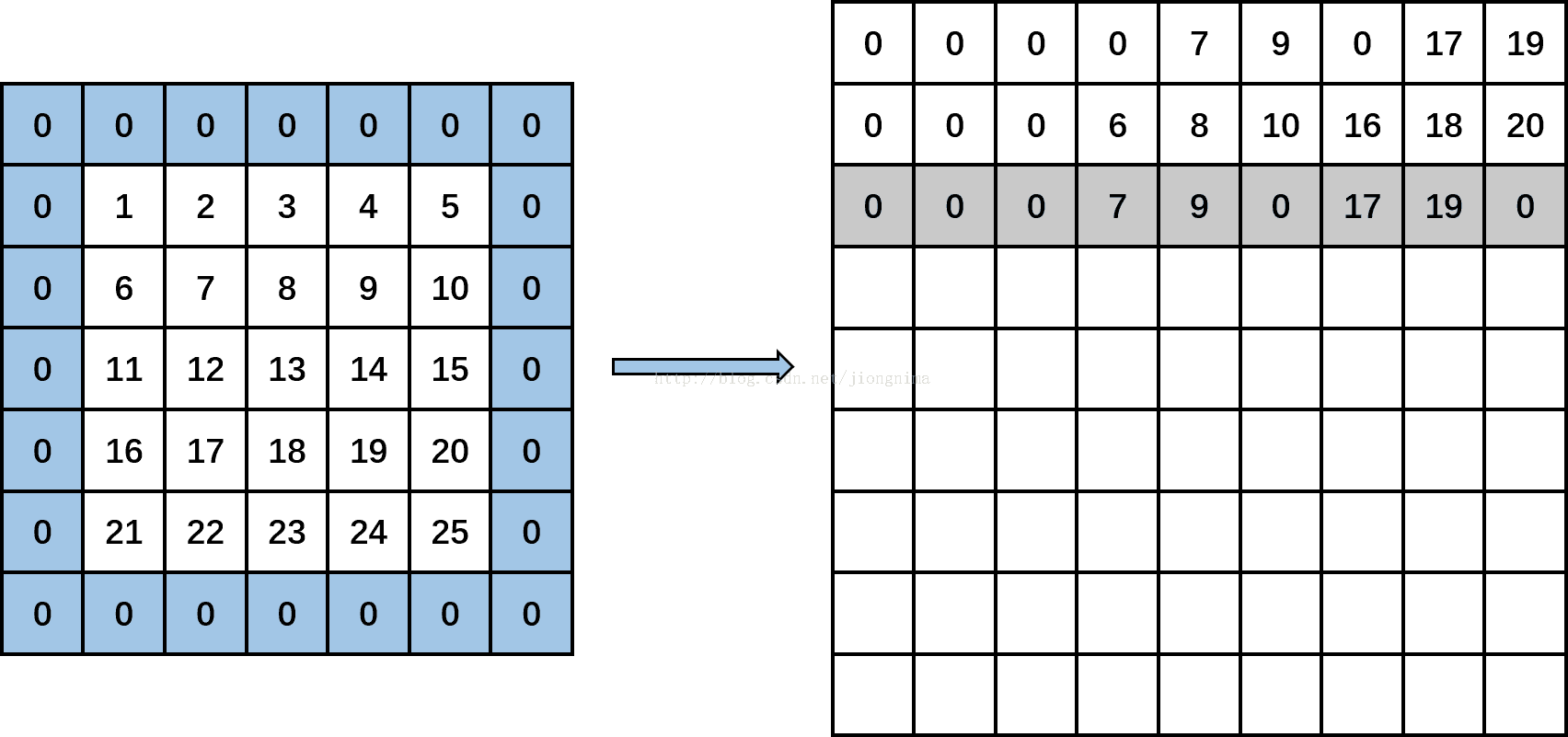
接着，kernel_row变成1，kernel_col变成0。计算input_row又变成0，input_col分别为-1(-1+0)，1(-1+0+2)和3(-1+0+2+2)，输出矩阵上分别输出0，data[0*5+1]，data[0*5+3]，即分别填入0,2,4。然后，input_row变成2，input_col分别为-1，1和3时，输出矩阵上分别输出0，data[2*5+1]，data[2*5+3]，即分别填入0,12,14。然后，input_row变成4，input_col分别为-1，1，3时，输出矩阵上分别输出0，data[4*5+1]，data[4*5+3]，即分别输出0,22,24。见下图：（将第一个通道的卷积对应第四个对应位置进放好）

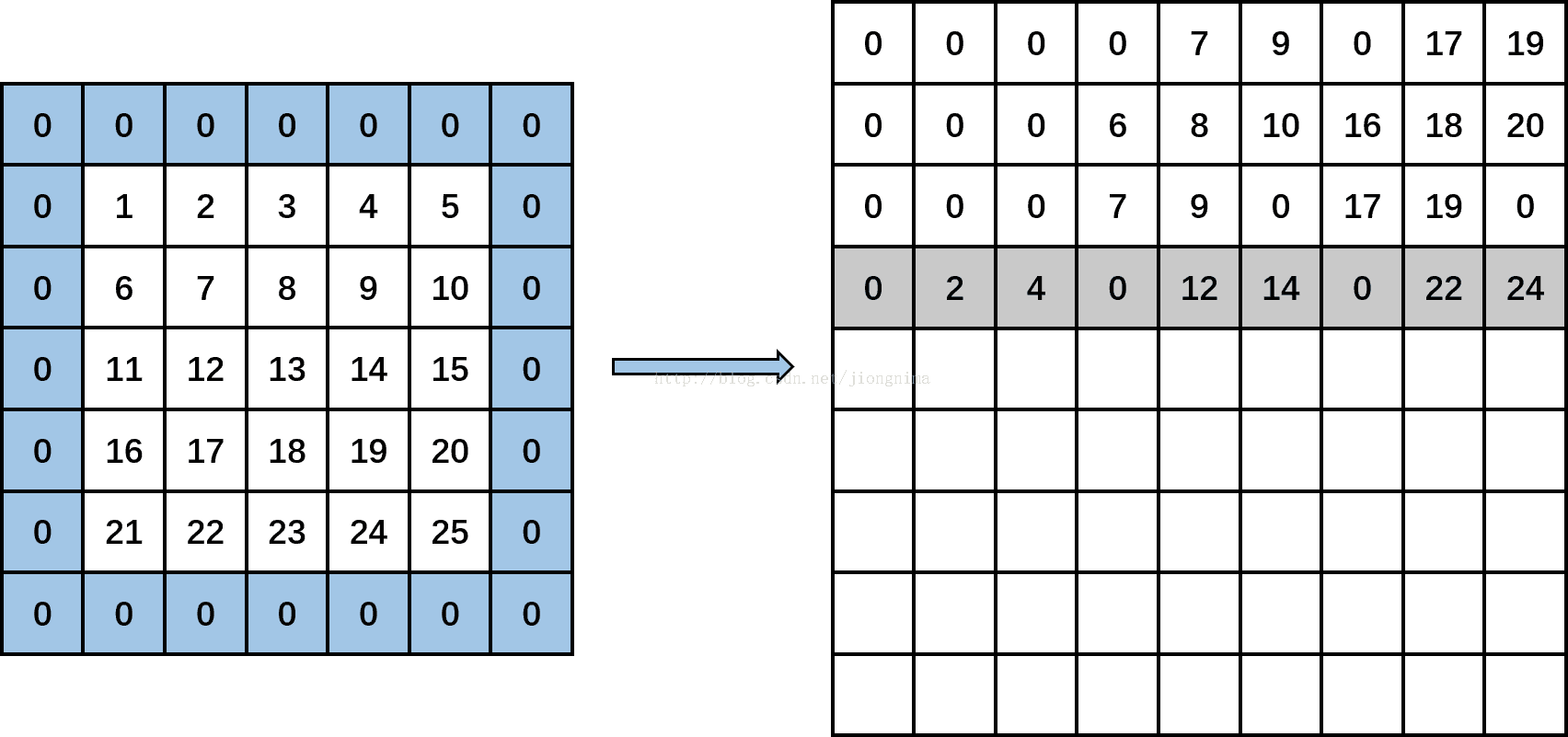
然后，kernel_row为1，kernel_col变成1。计算input_row为0，input_col分别为0(-1+1)，2(-1+1+2)和4(-1+1+2+2)，输出矩阵上分别输出data[0*5+0]，data[0*5+2]，data[0*5+4]，即分别填入1,3,5。然后，input_row变成2，input_col分别为0，2和4时，输出矩阵上分别输出data[2*5+0]，data[2*5+2]，data[2*5+4]，即分别填入11,13,15。然后，input_row变成4，input_col分别为0，2，4时，输出矩阵上分别输出data[4*5+0]，data[4*5+2]，data[4*5+4]，即分别输出21,23,25。见下图：（将第一个通道的卷积对应第五个对应位置进放好）

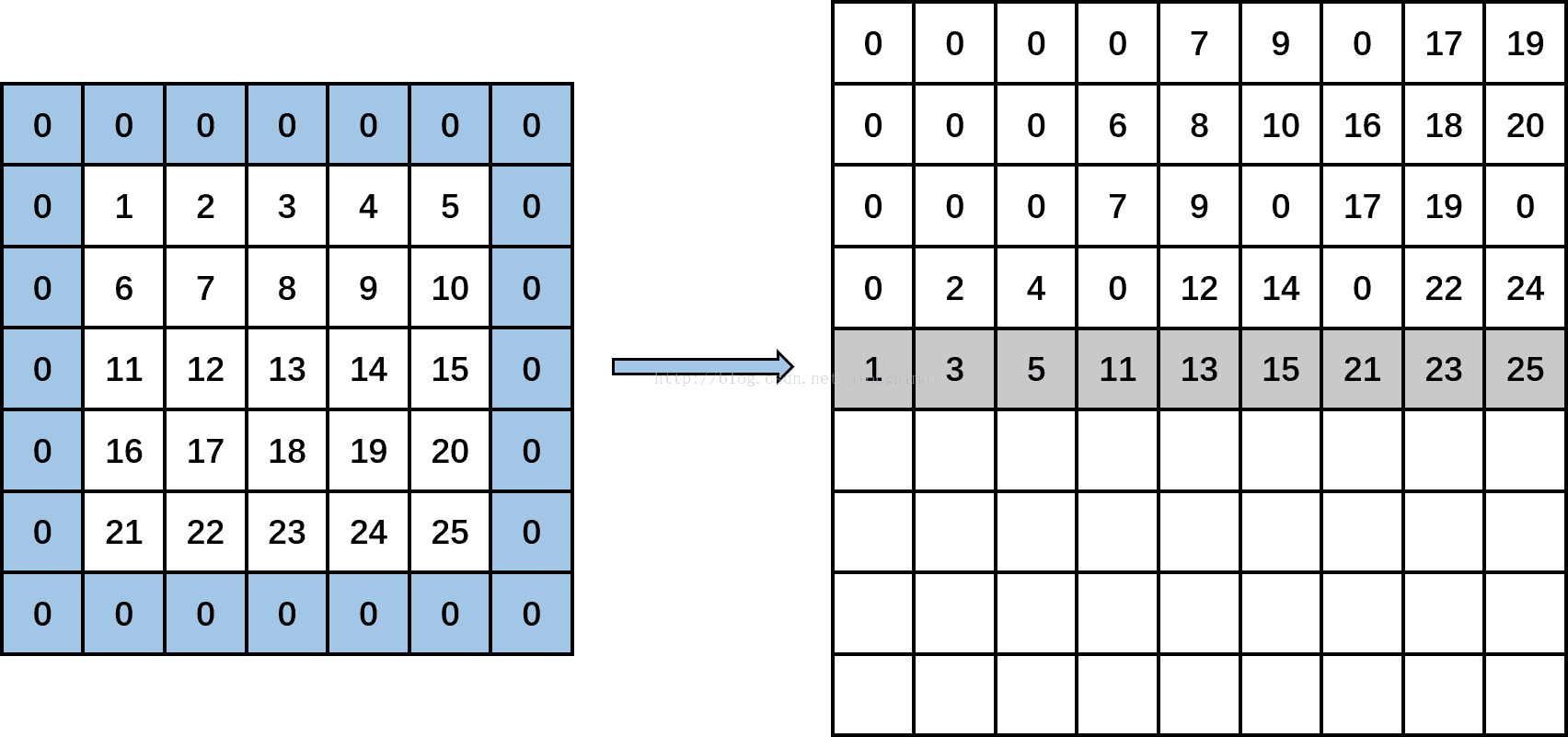
然后，kernel_row为1，kernel_col变成2。计算input_row为0，input_col分别为1(-1+2)，3(-1+2+2)和5(-1+2+2+2)，输出矩阵上分别输出data[0*5+1]，data[0*5+3]，0，即分别填入2,4,0。然后，input_row变成2，input_col分别为1，3和5时，输出矩阵上分别输出data[2*5+1]，data[2*5+3]，0，即分别填入12,14,0。然后，input_row变成4，input_col分别为1，3，5时，输出矩阵上分别输出data[4*5+1]，data[4*5+3]，0，即分别输出22,24,0。见下图：（将第一个通道的卷积对应第六个对应位置进放好）

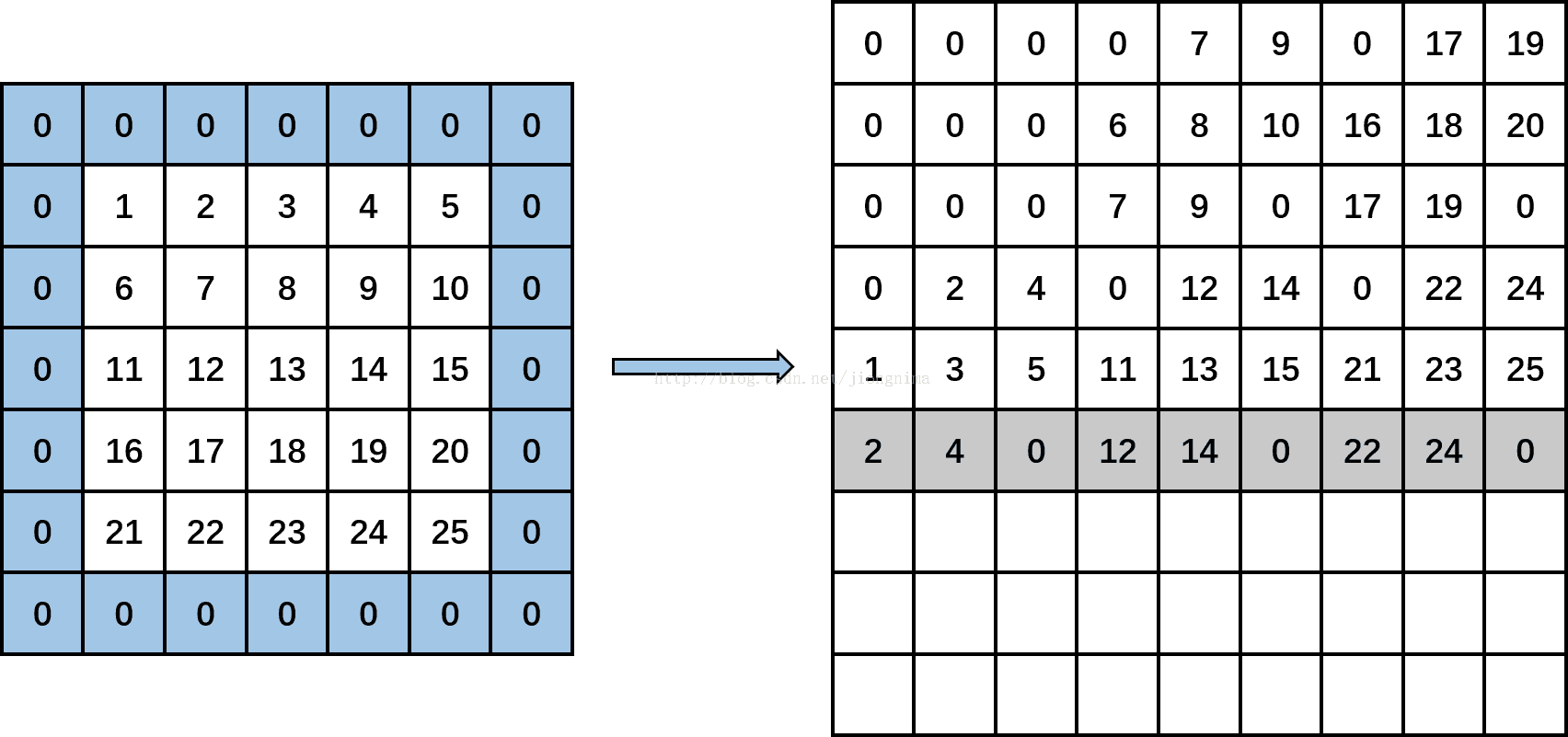
接着，kernel_row变成2，kernel_col变成0。计算input_row为1，input_col分别为-1(-1+0)，1(-1+0+2)和3(-1+0+2+2)，输出矩阵上分别输出0，data[1*5+1]，data[1*5+3]，即分别填入0,7,9。然后，input_row变成3，input_col分别为-1，1和3时，输出矩阵上分别输出0，data[3*5+1]，data[3*5+3]，即分别填入0,17,19。然后，input_row变成5，满足第一个if条件，直接输出三个0。见下图：（**将第一个通道的卷积对应第七个对应位置进放好）

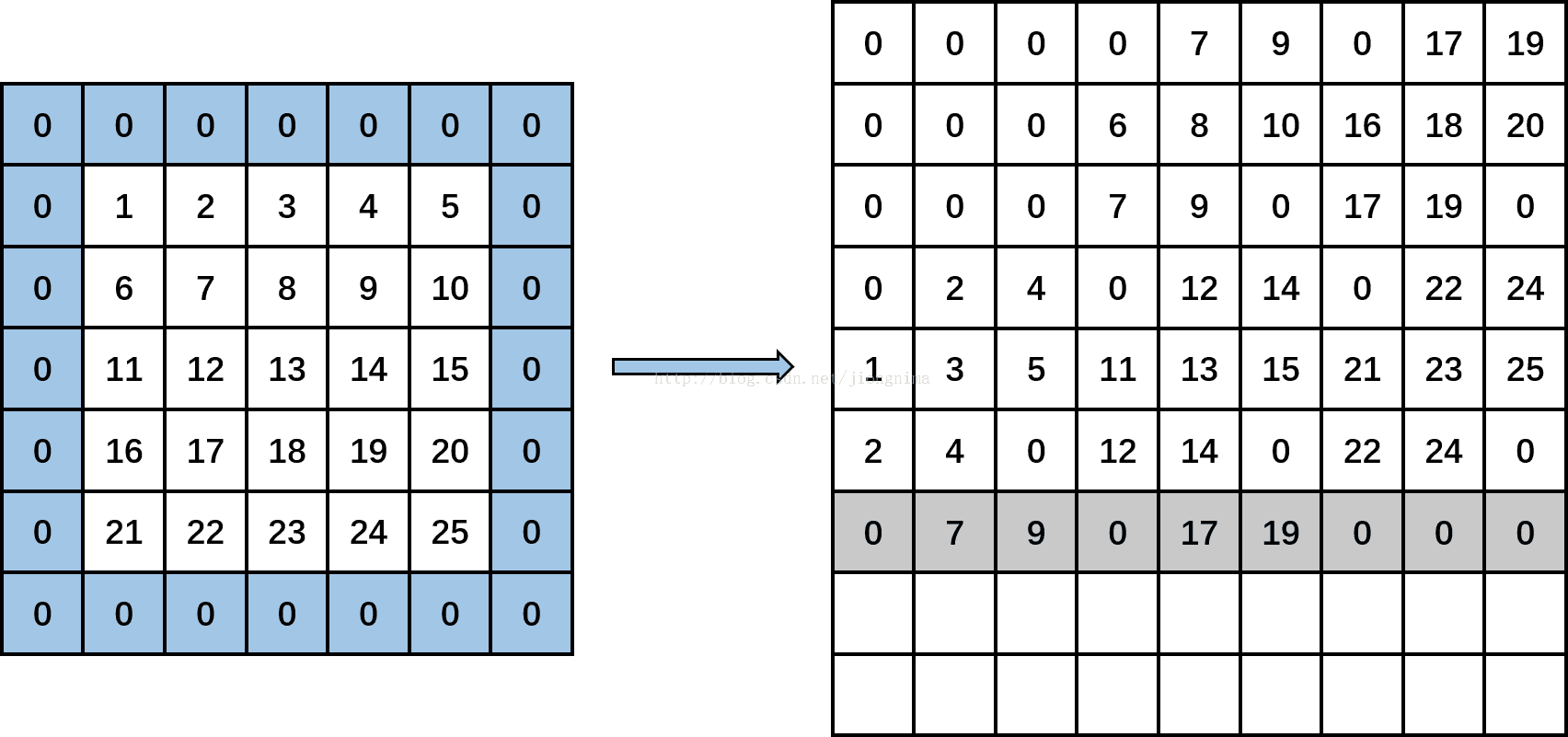
然后，kernel_row为2，kernel_col变成1。计算input_row为1，input_col分别为0(-1+1)，2(-1+1+2)和4(-1+1+2+2)，输出矩阵上分别输出data[1*5+0]，data[1*5+2]，data[1*5+4]，即分别填入6,8,10。然后，input_row变成3，input_col分别为0，2和4时，输出矩阵上分别输出data[3*5+0]，data[3*5+2]，data[3*5+4]，即分别填入16,18,20。然后，input_row变成5，满足第一个if条件，直接输出三个0。见下图：（将第一个通道的卷积对应第八个对应位置进放好）

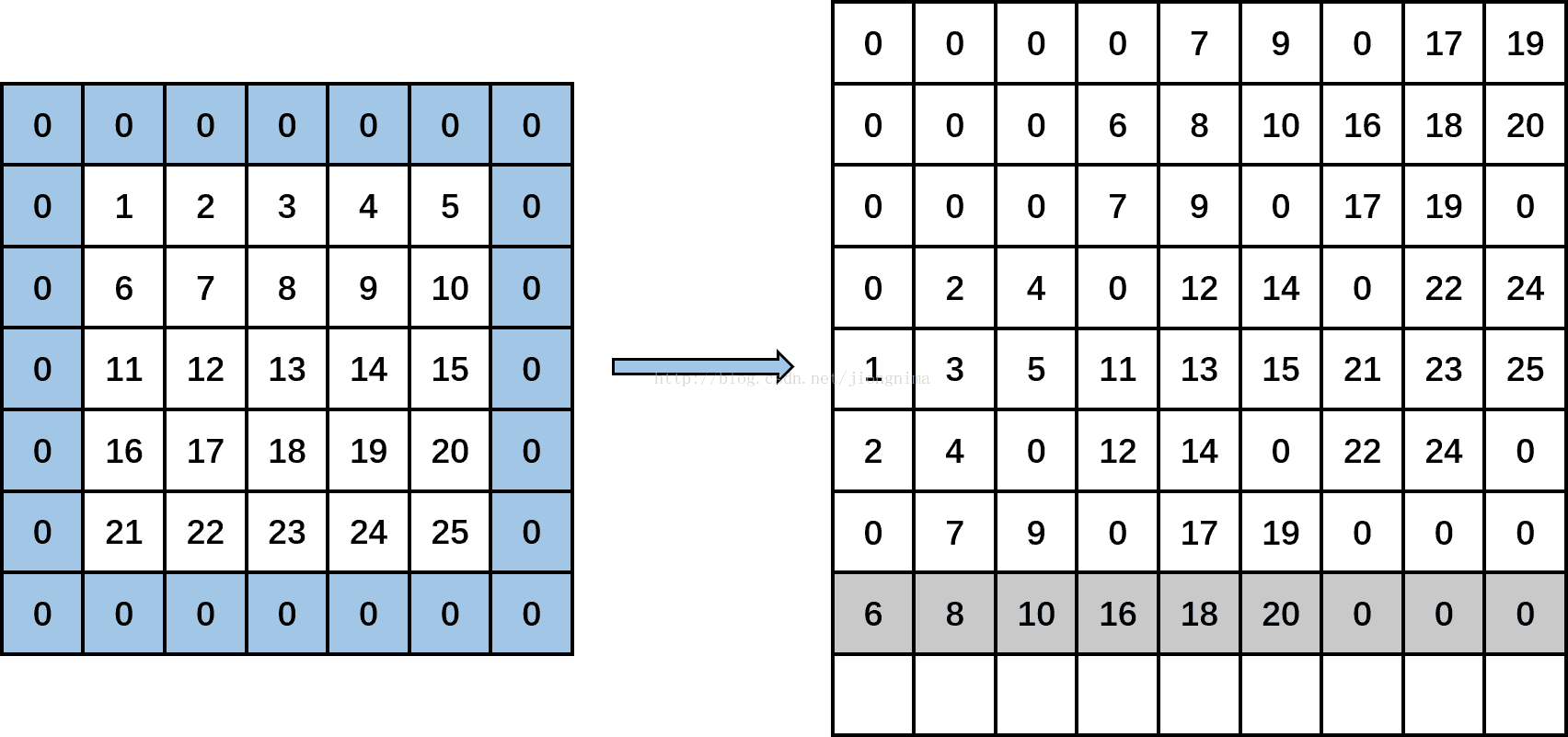
最后，kernel_row为2，kernel_col变成2。计算input_row为1，input_col分别为1(-1+2)，3(-1+2+2)和5(-1+2+2+2)，输出矩阵上分别输出data[1*5+1]，data[1*5+3]，0，即分别填入7,9,0。然后，input_row变成3，input_col分别为1，3和5时，输出矩阵上分别输出data[3*5+1]，data[3*5+3]，0，即分别填入17,19,0。然后，input_row变成5，满足第一个if条件，直接输出三个0。见下图：（将第一个通道的卷积对应第五个对应位置进放好）

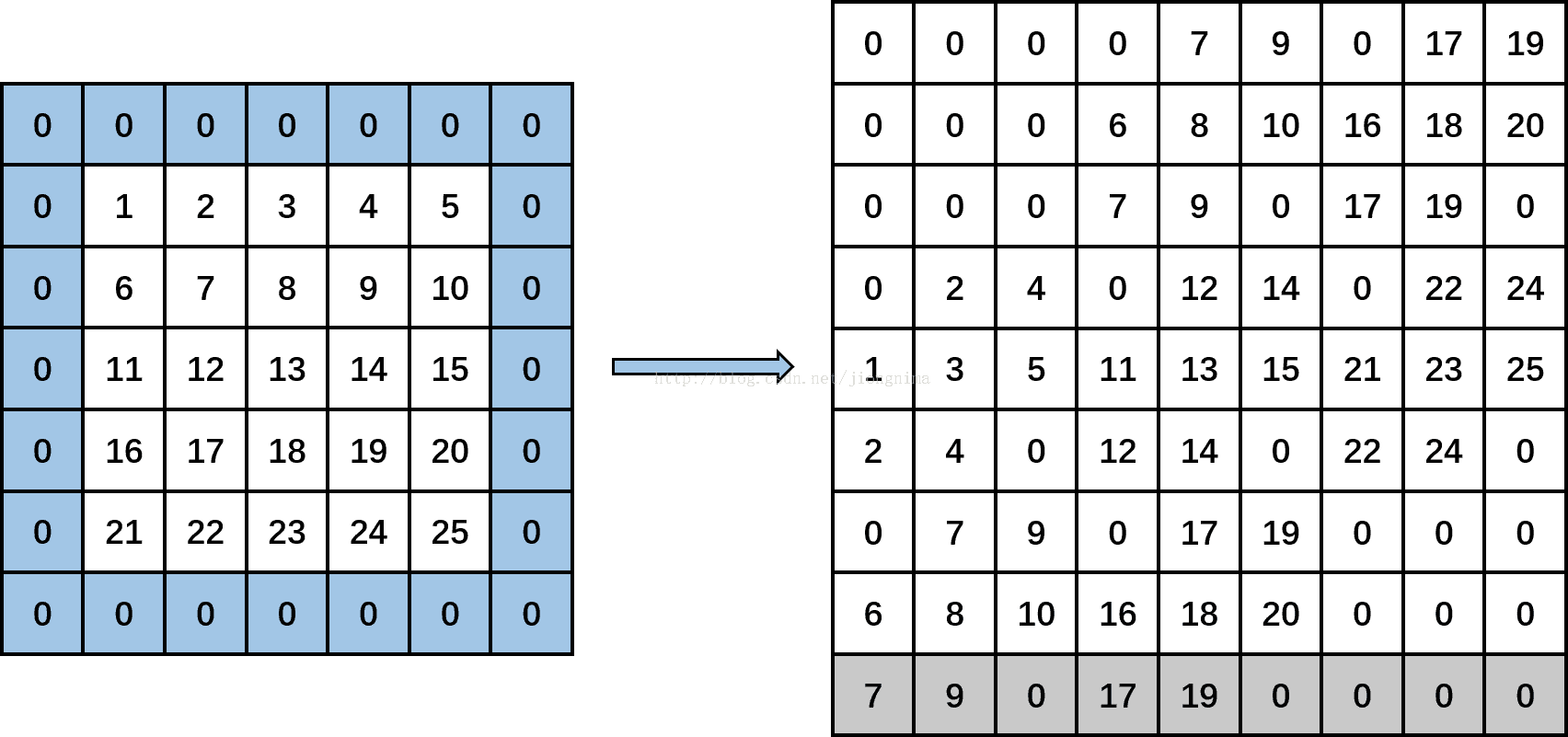
到此卷积层单通道输入特征图就转化成了一个矩阵，请读者朋友们仔细看看，矩阵的各列就是卷积核操作的各小窗口。

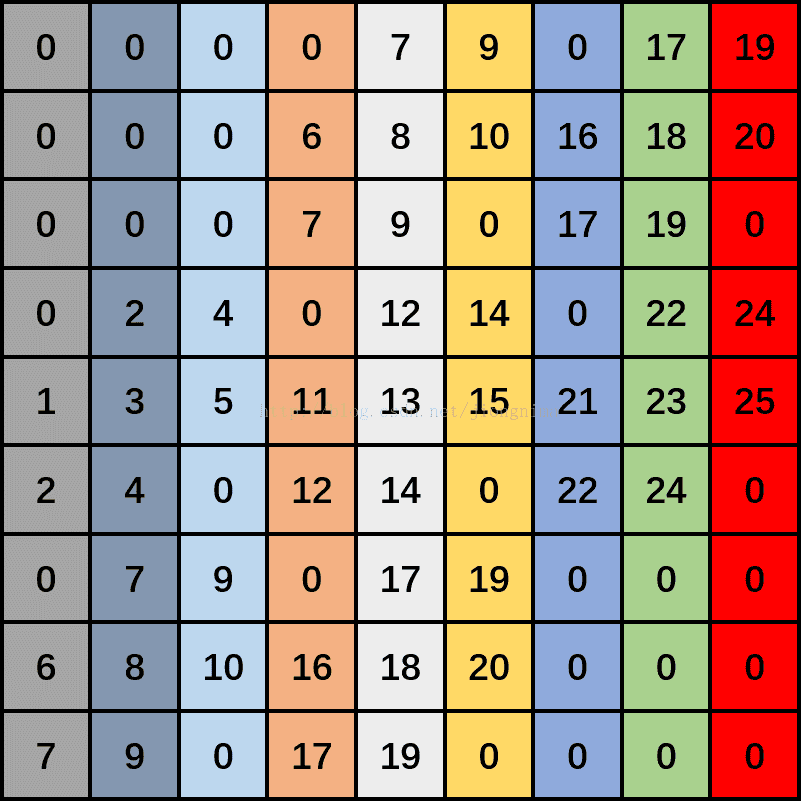
!!! 注意点：

（1）如果是多个通道的话，就要将其他通道放置在这个通道的下面，最终的结果是生成矩阵的每一列对应一个卷积核(多个通道)。

（2）卷积中的zero-padding操作的实现，并不是真正在原始输入特征图周围添加0，而是在特征图转化得到的矩阵上的对应位置添加0。

（3）这种算法的核心点在于，先去找卷积核(单通道)对应所有卷积结果对应的某个位置的像素值，将其放置在一行，从而完整单通道的复制。当然也可以找到某个卷积核(单通道)对应的位置，将其拉伸为列。

而im2col_cpu函数功能的相反方向的实现则有由col2im_cpu函数完成，笔者依旧把该函数的代码注释放在下面：

/*col2im_cpu为im2col_cpu的逆操作接收13个参数，分别为输入矩阵数据指针(data_col)，卷积操作处理的一个卷积组的通道 数(channels)，输入图像的高(height)与宽(width)，原始卷积核的高(kernel_h)与宽(kernel_w)， 输入图像高(pad_h)与宽(pad_w)方向的pad，卷积操作高(stride_h)与宽(stride_w)方向的步长， 卷积核高(stride_h)与宽(stride_h)方向的扩展，输出图像数据指针(data_im)*/  
template <typename Dtype>  
void col2im_cpu(const Dtype* data_col, const int channels,  
    const int height, const int width, const int kernel_h, const int kernel_w,  
    const int pad_h, const int pad_w,  
    const int stride_h, const int stride_w,  
    const int dilation_h, const int dilation_w,  
    Dtype* data_im) {  
    caffe_set(height * width * channels, Dtype(0), data_im);   //首先对输出的区域进行初始化，全部填充0  
    const int output_h = (height + 2 * pad_h - (dilation_h * (kernel_h - 1) + 1)) / stride_h + 1;  //计算卷积层输出图像的宽  
    const int output_w = (width + 2 * pad_w - (dilation_w * (kernel_w - 1) + 1)) / stride_w + 1;  //计算卷积层输出图像的高  
    const int channel_size = height * width;   //col2im输出的单通道图像容量
  
    for (int channel = channels; channel--; data_im += channel_size) {//按照输出通道数一个一个处理  
        for (int kernel_row = 0; kernel_row < kernel_h; kernel_row++) {  
            for (int kernel_col = 0; kernel_col < kernel_w; kernel_col++) {  
            int input_row = -pad_h + kernel_row * dilation_h;//在这里找到卷积核中的某一行在输入图像中的第一个操作区域的行索引  
         for (int output_rows = output_h; output_rows; output_rows--) {  
             if (!is_a_ge_zero_and_a_lt_b(input_row, height)) {//如果计算得到的输入图像的行值索引小于零或者大于输入图像的高(该行为pad)  
                data_col += output_w;  //那么，直接跳过这output_w个数，这些数是输入图像第一行上面或者最后一行下面pad的0  
             } else {  
                 int input_col = -pad_w + kernel_col * dilation_w;//在这里找到卷积核中的某一列在输入图像中的第一个操作区域的列索引  
                 for (int output_col = output_w; output_col; output_col--) {  
                      if (is_a_ge_zero_and_a_lt_b(input_col, width)) {//如果计算得到的输入图像的列值索引大于等于于零或者小于输入图像的宽(该列不是pad)  
                      data_im[input_row * width + input_col] += *data_col;//将矩阵上对应的元放到将要输出的图像上  
                 } //这里没有else，因为如果紧挨的if条件不成立的话，input_row*width + input_col这个下标在data_im中不存在，同时遍历到data_col的对应元为0  
                 data_col++;//遍历下一个data_col中的数  
                 input_col += stride_w;//按照宽方向步长遍历卷积核上固定列在输入图像上滑动操作的区域  
             }  
          }  
          input_row += stride_h;//按照高方向步长遍历卷积核上固定行在输入图像上滑动操作的区域  
             }  
            }  
        }  
    }  
}