​ 对于一个深度学习问题， 我们应该尽量从模型、数据、算法三个方向进行处理。对于目标检测也不例外。 这里，我们将从模型、数据和算法三个角度对目标检测这个问题进行展开探讨。 由于很多问题都是行业内有待讨论，值得商榷的， 所以一些观点也会附上链接， 并挑选出笔者认为合适的方案。

一. 模型部分：

一个典型的目标检测的前向推理流程为：

输入图像 → 提取特征 → 特征融合 → 解析为 bbox → nms → result

目标检测训练的典型流程为：

输入图像 → 提取特征→ 特征融合 → 解析为 bbox → bbox 匹配 → 计算 loss 并反向传播

在此以 YOLOv3 为例， 来探讨一下检测模型的几个核心部分：

• 网络主体框架：包括特征提取 backbone、特征融合 neck、特征输出 head
• nms
• loss 损失

1. 网络主体框架

一般分为三个部分： backbone、neck、head

（1）backbone：常见的 backbone 设计方案有

• 基础网络：VGG16、Resnet50、CSPReNeXt50、resnet50-vd
• Efficientnet、HRNet、SpineNet
• 轻量级网络：shufflenet、mobilenet、ghostnet

一些特殊结构： DCN、CoordConv、swish 或 mish 激活函数、Attention module（空间或者通道）、transformer 结构

(2) neck

addition-aggregation：SPP 模块、ASPP 模块、RFB 模块和 SAM 模块

Path-aggregation：FPN、PANet、NAS-FPN、 FC-FPN、BiFPN、ASFF、 SFAM

(3) head

主要是用于输出结果，一般为常见的卷积层

• Dense Prediction(one-stage):
  • RPN、SSD/YOLO、RetinaNet(anchor based)
  • CornerNet、CenterNet、MatrixNet、FCOS(anchor free)

• Sparse Prediction(two stage)

  • Faster RCNN、F-FCN、Mask R-CNN(anchor based)
  • RepPoints(anchor free)

• 单个 Anchor 分配多个标签

其他：更好的预训练模型

2. nms 设计

nms 设计要点在于判定两个 bbox 的 IoU。常见的 IoU 如下所示：

2.1 IoU

IoU就是我们所说的交并比，是目标检测中最常用的指标。 他的作用不仅用来确定正样本和负样本，还可以用来评价输出框 (predict box) 和 ground-truth 的距离。

$$IoU = \frac{A \cup B}{ A \cap B}$$

其拥有几个特性：

• 尺度不变形， 也就是说对尺度不敏感(scale invariant)。
• 度量的三要素：非负性、对称性、三角不等式。

IoU 存在的问题：

• 如果两个框没有相交，根据定义，IoU=0，不能反映两者的距离大小( 重合度 )。同时因为 loss=0，没有梯度回传，无法进行学习训练。
• IoU 无法精确的反映两者的重合度大小。如下图所示，三种情况IoU都相等，但看得出来他们的重合度是不一样的，左边的图回归的效果最好，右边的最差。

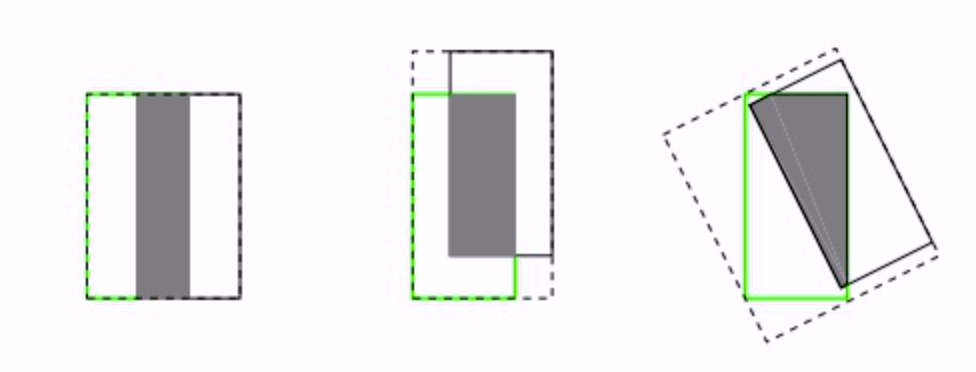
代码实现如下：

def IoU(box1, box2):
    """ box1, box2: top, left, bottom, right """
    area1 = (box1[2] - box1[0]) * (box1[3] - box1[1])
    area2 = (box2[2] - box2[0]) * (box2[3] - box2[1])
    
    in_h = min(box1[2], box2[2]) - max(box1[0], box2[0])
    in_w = min(box1[3], box2[3]) - max(box1[1], box2[1])
    
    inter = 0 if (in_h < 0 or in_w < 0) else in_h * in_w
    return inter / (area1 + area2 - inter)

2.2 GIoU

论文地址: https://arxiv.org/pdf/1902.09630.pdf

​ GIoU（Generalized Intersection over Union）相较于 IoU 多了一个 ‘Generalized’，这也意味着它能在更广义的层面上计算IoU，并解决刚才我们说的 ‘两个图像没有相交时，无法比较两个图像的距离远近’ 的问题。

GIoU 的计算公式为：

$$GIoU = IoU - \frac{A^c - (A \cup B)}{ A^c}$$

其中 $A^c$ 代表两个图像的最小包络面积，也可以理解为这两个图像的最小外接矩形的面积。由此我们可以看出：

• 原有 IoU 取值区间为 [0,1]，而 GIoU 的取值区间为 [-1,1]；在两个图像完全重叠时，IoU = GIoU = 1，在两个图像距离无限远时，IoU = 0 而 GIoU = -1。
• 与IoU只关注重叠区域不同，GIoU不仅关注重叠区域，还关注非重叠区域，这样能更好的的反映两个图像的重合度。其完善了图像的重叠度的计算功能。

代码实现如下：

def GIoU(box1, box2):
    """ box1, box2: top, left, bottom, right """
    area1 = (box1[2] - box1[0]) * (box1[3] - box1[1])
    area2 = (box2[2] - box2[0]) * (box2[3] - box2[1])
    
    in_h = min(box1[2], box2[2]) - max(box1[0], box2[0])
    in_w = min(box1[3], box2[3]) - max(box1[1], box2[1])
    inter = 0 if (in_h < 0 or in_w < 0) else in_h * in_w
    union = area1 + area2 - inter 
    
    iou = inter / union 
    
    area_C = ((max(box1[1], box1[3], box2[1], box2[3]) - min(box1[1], box1[3], box2[1], box2[3])) * 
              (max(box1[0], box1[2], box2[0], box2[2]) - min(box1[1], box1[3], box2[1], box2[3])))
    
  
    return iou - (area_C - union) / area_C

2.3 DIoU

参考论文：Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression

​ GIoU 虽然解决了 IoU 的一些问题(这里主要是重叠度的问题)，但是它并不能直接反映预测框与目标框之间的距离，比如当目标框完全包裹预测框的时候，IoU 和 GIoU 的值都一样，此时 GIoU 退化为IoU, 无法区分其相对位置关系。

DIoU(Distance-IoU)即可解决这个问题，它将两个框之间的重叠度、距离、尺度都考虑了进来，DIoU的计算公式如下：

$$DIoU = IoU - \frac{\rho^2(b, b^{gt})}{c^2}$$

其中 $b$，$b^{gt}$ 分别代表两个框的中心点， $rho$ 代表两个中心点之间的欧氏距离，$c$ 代表最小包络矩形的对角线，即如下图所示：

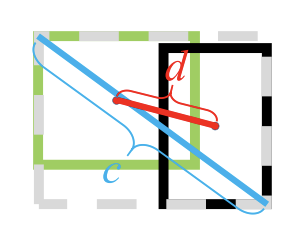
DIoU 相较于其他两种计算方法的优点是：

• DIoU 可直接最小化两个框之间的距离，所以作为损失函数的时候 loss 收敛的更快；
• 在两个框完全上下排列或左右排列时，没有空白区域，此时 GIoU 几乎退化为了 IoU，但是 DIoU 仍然有效。

我们可以认为，DIoU 在完善图像重叠度的计算功能的基础上，实现了对图形距离的考量，但仍无法对图形长宽比的相似性进行很好的表示。

代码实现如下：

def DIoU(box1, box2):
    """ box1, box2: top, left, bottom, right """
    C_2 = ((max(box1[1], box1[3], box2[1], box2[3]) - min(box1[1], box1[3], box2[1], box2[3])) ** 2 + 
           (max(box1[0], box1[2], box2[0], box2[2]) - min(box1[1], box1[3], box2[1], box2[3])) ** 2)
    
    D_2 = (((box2[1]+box2[3])/2 - (box1[1]+box1[3])/2)**2 + 
         ((box2[0]+box2[2])/2 - (box1[0]+box1[2])/2)**2)
 
    iou = IoU(box1, box2)
    return iou - D_2 / C_2

2. 4 CIoU

CIoU 的全称为 Complete IoU，它在 DIoU 的基础上，还能同时考虑两个矩形的长宽比，也就是形状的相似性，CIoU 的计算公式为：

$$CIoU = IoU - \frac{\rho^2(b, b^{gt})}{c^2} - \alpha v$$

其中 $\alpha$ 是权重参数，而 $v$ 用来度量长宽比的相似性：

$$v = \frac{4}{\pi^2} (arctan \frac{w^{gt}}{h^{gt}} - arctan \frac{w}{h})^2, \\ \alpha = \frac{v}{(1-IoU) + v }$$

可以看出，CIoU 就是在 DIoU 的基础上，增加了图像相似性(长宽比)的影响因子，因此可以更好的反映两个框之间的差异性。

代码实现如下：

import math

def CIoU(box1, box2):
    """ box1, box2: top, left, bottom, right """
    iou = IoU(box1, box2)
    diou = DIoU(box1, box2)

    v = 4 / math.pi**2 * (math.atan((box2[3] - box2[1])/(box2[2] - box2[0])) 
                         - math.atan((box1[3] - box1[1])/(box1[2] - box1[0])))**2 + 1e-5
    alpha = v / ((1-iou) + v)
    return diou - alpha * v

如下图所示， 是以不同的 IoU 作为损失函数， 在 Pascal VOC 验证集上的增益：

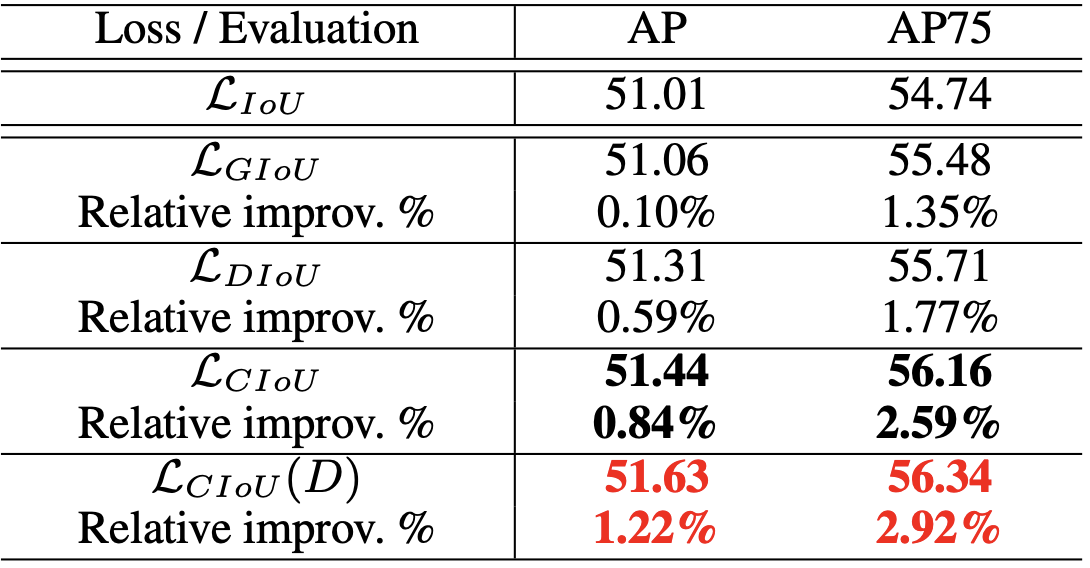
2.5 Matrix nms

3. loss 设计

目标检测中的损失函数 loss 可以分为两类： 第一类是分类损失， 第二类是检测回归损失。

常见的分类损失有： cross entropy、 focal loss、GHM loss、AP loss 和 DR loss 等等

常见的回归损失有：

• l1、l2、smooth l1
• IOU loss
• 其他本文未展开 loss： softer nms 的 KL loss、 GHM-R loss、IoU-bounded loss、 huber loss 的概率解释新 loss， libra RCNN 的 balanced l1 loss

3.1 分类损失

3. 1.1 cross entropy 交叉熵损失

交叉熵损失是我们再计算分类损失的时候最常用的损失函数， 其公式如下：

$$CE = \left\{ \begin{aligned} -log(p) , && if \ \ y = 1 \\ -log(1-p),&& if \ \ y = 0 \end{aligned} \right.$$

单阶段的目标检测器通常会产生高达 100k 的候选目标， 只有极少数是正样本， 正负样本数量非常不平衡。 为了解决正负样本不平衡的问题， 我们通常会在交叉熵损失的前面加上一个参数 $\alpha$, 即:

$$CE = \left\{ \begin{aligned} -\alpha log(p) , && if \ \ y = 1 \\ -(1-\alpha)log(1-p),&& if \ \ y = 0 \end{aligned} \right.$$

3.1. 2 focal Loss

​ focal loss 的引入主要是为了解决难以样本数量不平衡（注意， 有区别于正负样本数量不平衡）的问题。在目标检测算法中，添加权重 $\alpha$ 平衡了正负样本的数量， 但是对于难易样本的不平衡并无助益。 实际上，易分样本对模型的提升效果非常小， 模型应该主要关注那些难分对象。 (这个观点有问题， 是 GHM 的主要改进对象)。 focal loss 的提出主要是为了解决难易样本数量的不平衡问题。其思路很简单： 把高置信度 $p$ 样本的损失降低一些即可:

$$CE = \left\{ \begin{aligned} -(1-p)^\gamma log(p) , && if \ \ y = 1 \\ -p^\gamma log(1-p),&& if \ \ y = 0 \end{aligned} \right.$$

举个例子， $\gamma $ 取 2， p 取 0.968 的时候， $(1-0.968)^2$ 约定于 0.001， 损失衰减了 1000 倍。 focal loss 的最终形式结合了正负样本的权重 $\alpha$ 和 难易样本的权重 $(1-p)^\gamma$。 同时解决了正负样本的不均衡和难易样本的不均衡问题。 最终的 focal loss 形式如下：

$$CE = \left\{ \begin{aligned} -\alpha (1-p)^\gamma log(p) , && if \ \ y = 1 \\ -(1-\alpha) p^\gamma log(1-p),&& if \ \ y = 0 \end{aligned} \right.$$

实验证明， 当 $\gamma$ 取 2， $\alpha$ 取 0.25 的时候效果最佳。

3.1.3 GHM

focal loss 存在两个问题： (1) 让模型过多的关注那些难分样本是存在问题的。 比如样本中有离群点， 那么模型已经收敛的模型还要去关注这些样本。 (2) 公式中的 $\alpha$ 和 $\gamma$ 的取值需要凭借试验得出， 且 $\alpha$ 和 $\beta$ 要联合起来一起试验才行。 GHM(gradient harmonizing mechaism) 解决了上述两个问题。

文章首先定义了一个梯度模长 g:

$$g = |p - p^*| = \left\{ \begin{aligned} (1-p) , && if \ \ p^* = 1 \\ p,&& if \ \ p^* = 0 \end{aligned} \right.$$

其中 $p$ 是模型预测的概率， $p^$ 是 ground-truth 的标签， $p^$ 的取值为 0 或 1。

g 正比于检测的难易程度， g 越大则检测难度越大。 注意到梯度模长和样本数量的关系如下图所示：

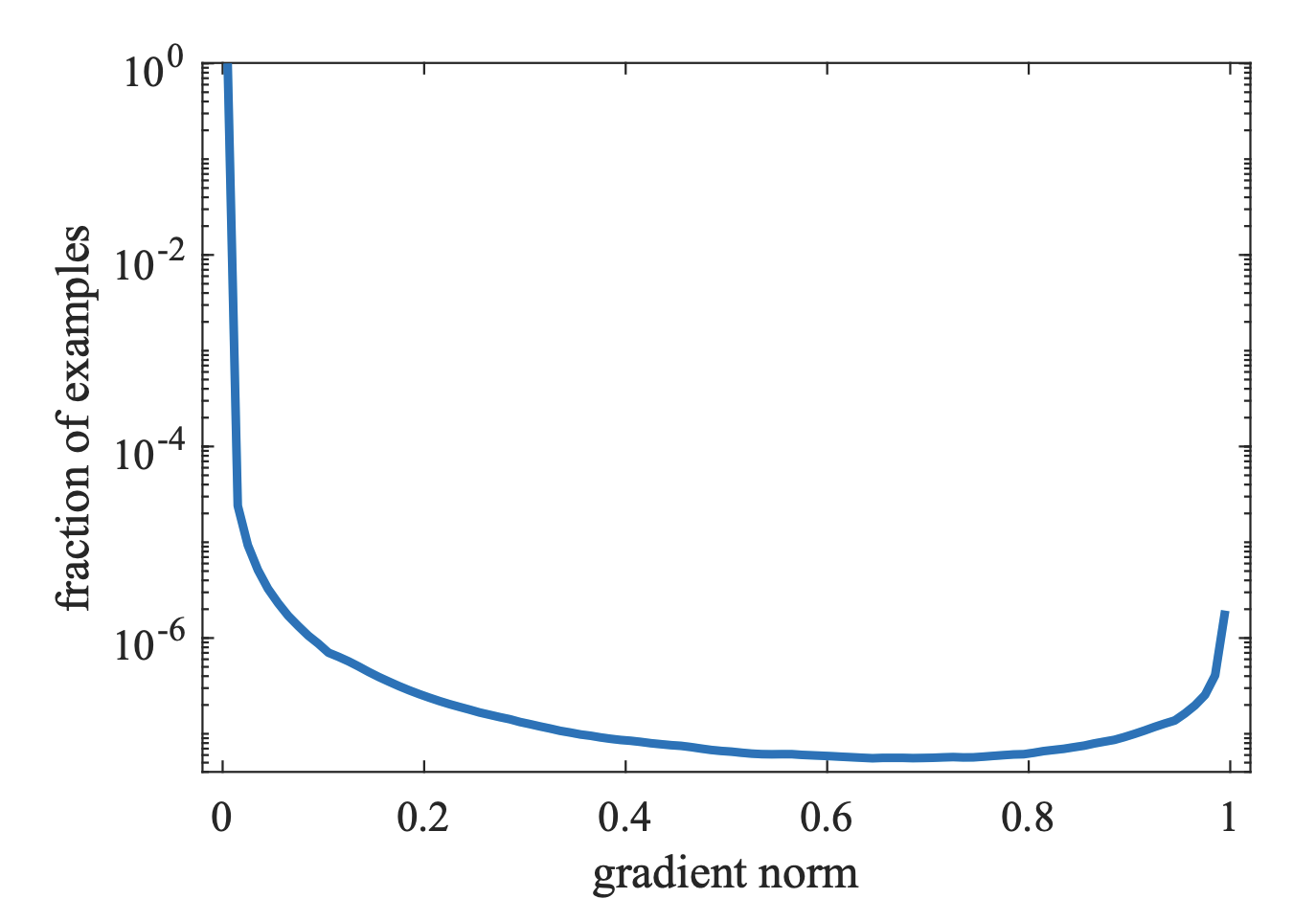
可以看到， 梯度模长接近于 0 的样本数量最多， 随着梯度模长的增长， 样本数量迅速减少， 但是在梯度模长接近于1 时， 样本数量也挺多。 GHM 的想法是， 我们确实应该如 focal loss 所说的不应该过分关系易分样本，但是特别难分的样本(outliers, 离群点) 也不该关注。所以作者认为应该同时衰减易分样本和难分样本， 区分的方法是定义了梯度密度 $GD(g)$ 这个变量， 来衡量出一定梯度范围内的样本数量。

$$GD(g) = \frac{1}{l_\varepsilon (g)} \sum_{k=1}^{N} \delta_\epsilon(g_k, g)$$

其中 $\delta\epsilon(g_k, g)$ 表明了样本 1- N 中， 梯度模长分布在 $(g-\frac{\epsilon}{2}, g+\frac{\epsilon}{2})$ 范围内的样本个数， $l\epsilon(g)$ 代表了 $(g-\frac{\epsilon}{2}, g+\frac{\epsilon}{2})$ 区间的长度。梯度密度的含义是：单位梯度模长 g 部分的样本个数。所谓的 GHM 损失 $l_{GHM-C}$ 就是 交叉熵CE 除以该样本的梯度密度即可。

$$L_{GHM-C} = \sum_{i=1}^{N} \frac{L_{CE}(p_i, p_i^*)}{GD(g_i)}$$

其实不同的损失函数都是对不同的样本赋予不同的权重， CE 中添加 $\alpha$ 是为了抑制负样本； focal loss 添加 $(1-p)^\gamma$ 则是用来抑制简单样本，而 GHM 则用来同时抑制简单样本和较困难样本。

3. 2. 回归损失

3. 2. 1 L2, L1, smooth L1

$$\begin{align} L_2(x) &= x^2 \\ L_1(x) &= |x| \\ smooth_{L1}(x) &= \left\{ \begin{aligned} 0.5x^2 &&if |x| < 1\\ |x| - 0.5& & otherwise\\ \end{aligned} \right. \end{align}$$

​ smooth L1 loss 相对于 l2 loss 的优点： 当预测框与 ground truth 差别过大时，梯度值不至于过大；当预测框与 ground truth 差别很小时，梯度值足够小。

3.2.2 IoU loss

​ 首次将 IoU 的概念引入 loss 损失函数由旷视提出， 发表于 UnitBox: An Advanced Object Detection Network。 论文指出，通过 4 个点回归坐标框的方式是假设4个坐标点是相互独立的，没有考虑其相关性，实际 4 个坐标点具有一定的相关性。其中 $IoU_{loss} = 1 - IoU + 修正项$。其中， IoU 可以是 IoU， GIoU， DIoU 和 CIoU。

3.2.3 IOU Aware

3.2.4 Grid Sensitive

二. 数据增强技术(含标签增强)

常见的数据增强方式可以分为四种： 几何变换、光学变换、增强噪声、数据源扩充。

• 几何变换：可以丰富物体在图像中出现的位置和尺度等， 从而满足模型的平移不变性与尺度不变性。例如平移， 翻转、翻转、缩放和裁剪等操作。尤其是水平翻转 180度， 在多个物体检测算法中都有使用， 效果很好。

• 光学变化：可以增加不同光照和场景下的图像， 典型的操作有亮度、对比度、色相与饱和度的随机扰动、通道色域之间的交换等。

• 增加噪声： 通过在原始图像上增加一定的扰动， 如高斯噪声。稍微复杂一点的就是在面积大小可选定、位置随机的矩形区域上丢弃像素产生黑色矩形块。 增加噪声可以使模型对可能遇到的噪声等自然扰动产生鲁棒性， 从而提升模型的泛化能力。 需要注意噪声不能过大， 以免影响模型的输出。上面的几何变换类操作，没有改变图像本身的内容，它可能是选择了图像的一部分或者对像素进行了重分布。如果要改变图像本身的内容，就属于颜色变换类的数据增强了，常见的包括噪声、模糊、颜色变换、擦除、填充等等。

• 数据源头： 有时为了扩充数据集， 可以将检测物体与其他背景图像融合，通过替换物体背景的方式来增加数据集的丰富性。 比如比较时髦的 CutOut、Mixup、CutMix、Mosaic、label-smoothing 等方案。

一些比较有用的数据增强方案的代码解析

dataset

1. data-aug:

• YOLOv4: CutMix、Mosaic （马赛克） 、Self Adversarial Training， SAT、Label Smoothing

• PPYolo: DropBlock

• freebies: Image Mixup、Label Smoothing

• mixup

1. big batchsize

2. random shapes training

3. 解决数据不平衡问题

4. freebies：Data Preprocessing

三. 算法优化

1. 学习率 done

>>> scheduler = ...
>>> for epoch in range(100):
>>>     train(...)
>>>     validate(...)
>>>     scheduler.step()

常见的几种学习率的调整方法： ReduceLROnPlateau、余弦退火、StepLR

• ReduceLROnPlateau：当指定指标不下降（上升）的时候， 将学习率降低为原来的十分之一。是这三种方案里面最优的， 他可以根据训练的情况进行动态调整， 需要注意的是， 用的时候最好设置一下最小学习率，不然后期会因为学习率衰减得过小导致模型不再训练。

  torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode='min', factor=0.1, patience=10, threshold=0.0001, threshold_mode='rel', cooldown=0, min_lr=0, eps=1e-08, verbose=False)

• 余弦退火使用的时候，最大学习率和最小学习率相差的数量级不要太大(比如1e-1和1e-4)，不然会导致在该快的时候太慢，该慢的时候太快，特别的接近最优解的时候，太大就直接跑偏

  torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max, eta_min=0, last_epoch=-1, verbose=False)

• StepLR 传统，也挺好用的，但是灵活度不如 ReduceLROnPlateau

  torch.optim.lr_scheduler.StepLR(optimizer, step_size, gamma=0.1, last_epoch=-1, verbose=False)

warmup：warmup 是在 resnet 论文中提到的一种学习率预热的方法，它在训练开始的时候先选择使用一个较小的学习率，训练了一些 epoches 或者 steps (比如 4 个epoches, 10000steps)， 再修改为预先设置的学习来进行训练。由于刚开始训练时，模型的权重(weights)是随机初始化的，此时若选择一个较大的学习率,可能带来模型的不稳定(振荡)，选择 Warmup 预热学习率的方式，可以使得开始训练的几个 epoches 或者一些 steps 内学习率较小，在预热的小学习率下，模型可以慢慢趋于稳定,等模型相对稳定后再选择预先设置的学习率进行训练,使得模型收敛速度变得更快，模型效果更佳

torch.optim.lr_scheduler.CosineAnnealingWarmRestarts(optimizer, T_0, T_mult=1, eta_min=0, last_epoch=-1, verbose=False)

​ 通常当我们增加 batchsize 为原来的 n 倍时，要保证经过同样的样本后更新的权重相等，按照线性缩放规则，学习率应该增加为原来的 n 倍[5]。但是如果要保证权重的方差不变，则学习率应该增加为原来的 sqrt(n) 倍[7]，目前这两种策略都被研究过，使用前者的明显居多。

2. 优化器 done

SGD with momentum 和 Adam variants 是最通用、最基本的选择。 计算机视觉任务优先使用前者， NLP 优先使用后者。原因是自适应优化器 adam 更容易找到 sharp minima， 泛化性能常常比 SGD 差。

torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0, amsgrad=False)

torch.optim.SGD(params, lr=<required parameter>, momentum=0, dampening=0, weight_decay=0, nesterov=False)

3. 归一化

常见的归一化方式如下图所示，其中 N 是 batch size， C 表示的是 channel， H 和 W 表示单张图片的宽度和高度, 蓝色区域的部分就是需要归一化的部分。

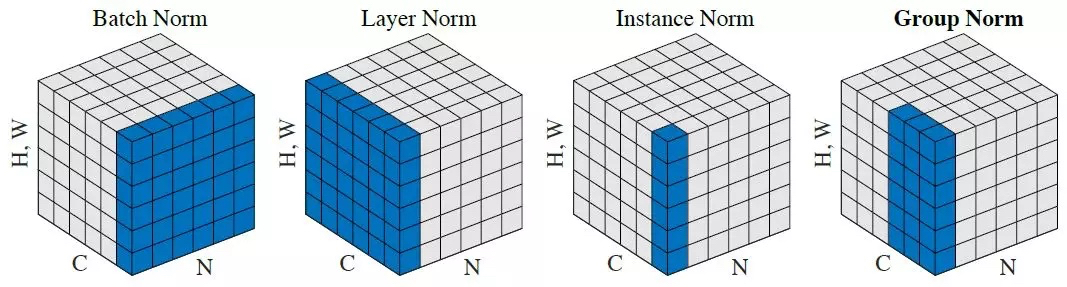
归一化步骤

• 计算归一化部分的均值 $\mu$，方差 $\sigma^2$ , 进行归一化 $x’ = \frac{x-\mu}{\sqrt{\sigma^2 + t}}$

• 加入缩放和平移变量 $\gamma$ 和 $\beta$， 归一化后的值 $y = \gamma x’ + \beta$

四个 Normalization 适用于不同的模型。 其中 Batch Normalization：适用于判别模型，比如图片分类。Instance Normalization 适用于生成模型，比如图片分割、迁移。Group Normalization 则是为了解决 Batch Normalization 对较小的 mini-batch 效果差的问题。 Layer Normlization 多用于 NLP 任务比如 RNN 和 Transformer。

? ? ? ? ? BN: CmBN/SyncBN

4. 初始化

网络参数初始化的优劣在极大程度上决定了网络的最终性能。网络参数初始化方式主要有以下几种：

• 全零初始化：全零初始化会导致神经元的输出相同，相同的输出导致梯度更新完全一样，这样便会令更新后的参数仍然保持一样的状态，从而无法对模型进行训练。
• 随机初始化：将参数值随机设定为接近0的一个很小的随机数（有正有负）。比如使用高斯分布或者均匀分布。比较推荐的模型包括： Xavier 初始化方式和 Kaiming 初始化方式。
• 预训练模型初始化
• 数据敏感的参数初始化方式 https://github.com/philkr/magic_init

5. 参数更新方案

遗传算法选择超参数

参数更新上使用滑动平均

四. 其他

1. 编写代码的基本流程

• 构建网络， 输入随机 Tensor， 检查输入和输出是否正确。
• 构建数据集读取接口， 查看是否能够准确的读取数据、可视化，并检测数据
• 编写损失函数、评价指标，优化方法
• 组合优化、数据和网络

2. 网络设计的考虑点

• 现有精度能否得到需求的指标
• 运算资源是否足够

五. 常见问题

1. 多尺度问题

我们总结了 6 种 有效解决多尺度问题的方案， 其中前四种是比较通用的提升多尺度检测的经典方法

（1） 降低下采样率和使用空洞卷积可以显著提高小物体的检测性能： 对于小物体检测而言， 降低网络的下采样率是最为简单的提升方式， 通常的做法是直接去掉 pooling 层。 如果仅仅去掉 pooling 层， 则后序层的感受野会较小， 由于后序层的感受野和预训练模型对应层的感受野不同， 从而会导致不能很好的收敛， 一个比较常见的做法是去掉 pooling 层后，将后序的一个 3x3 卷积变为 空洞数为 2 的卷积， 可以达到有效的降低下采样的目的。

（2） 设计更好的 anchor 可以有效提升 proposal 的质量：由于不同的数据集合任务中， 由于物体的尺度、大小会有所差异， 与通用的标签会有所区别， 这时需要调整 anchor 的大小和宽高。 一个比较经典的做法是 yolo 采用的 anchor 聚类算法。

（3）多尺度训练(MST, Multi Scale Training， MST)可以近似构建出图像金字塔， 增加样本的多样性：通常是指设置几种不同的图片输入尺度， 训练时从多个尺度中随机选取一种尺度， 将输入图片缩放到该尺度并送入网络中。 在测试中， 为了得到精准的检测效果，可以将测试图片的尺度放大， 例如放大 4 倍。 这样可以避免小物体的漏检。

（4） 特征融合可以构建出特征金字塔， 将浅层与深层特征优势互补：随着网络层数的增加， 感受野会增大，语义信息也更为丰富， 但是对于小物体， 其特征会随着层数的加深而逐渐丢失， 从而导致检测性能的降低。 将深浅层特征进行融合，可以实现底层特征和高层语义信息的融合。 常见的做法有： FPN的特征金字塔、 DetNet 的空洞卷积与残差、HyperNet 的反卷积与通道拼接、DSSD 的反卷积与特征相乘、RefineDet 的反卷积与逐元素相加， YOLOv3 的上采样与通道拼接。

（5） SNIP: SNIP 使用了累死 MST 的多尺度训练方法， 构建了 3 个 尺度的图像金字塔， 3 个尺度分别拥有各自的 RPN 模块， 各自预测指定范围内的物体。但是在训练时， 只对指定范围的 proposal 进行反向传播。

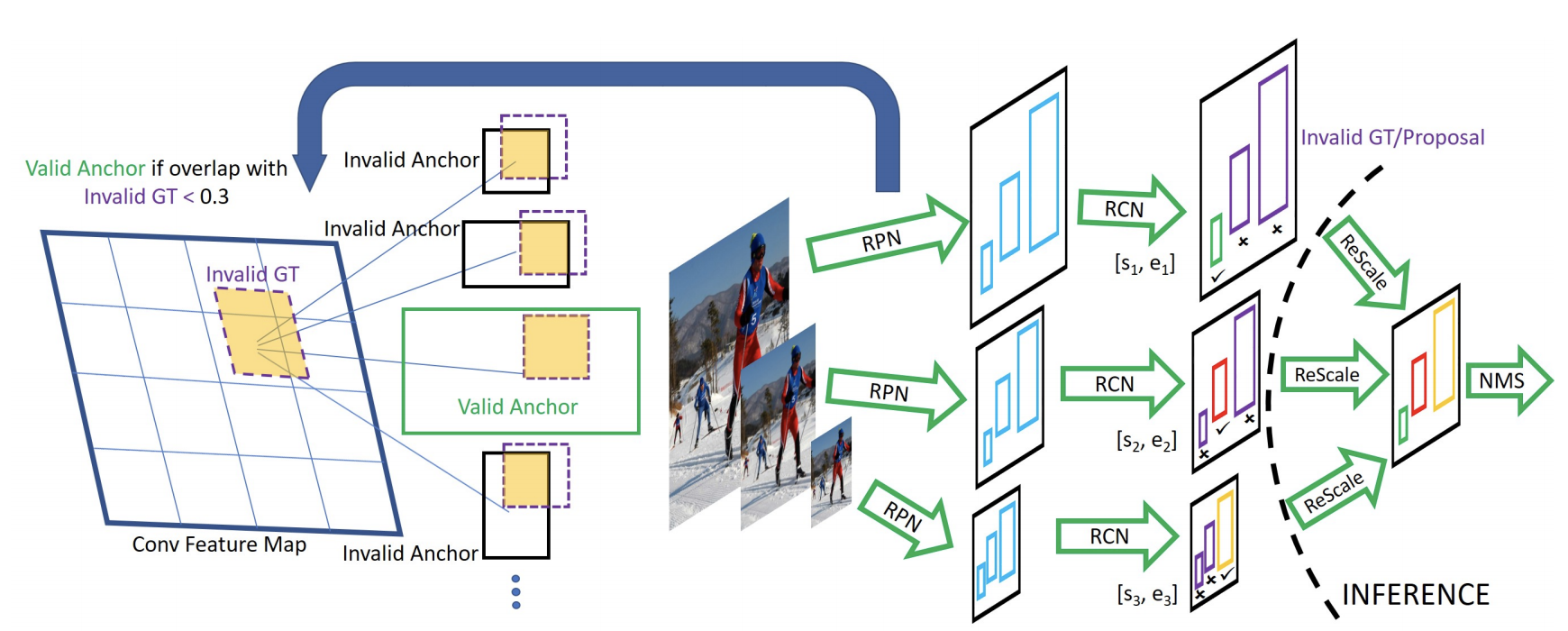
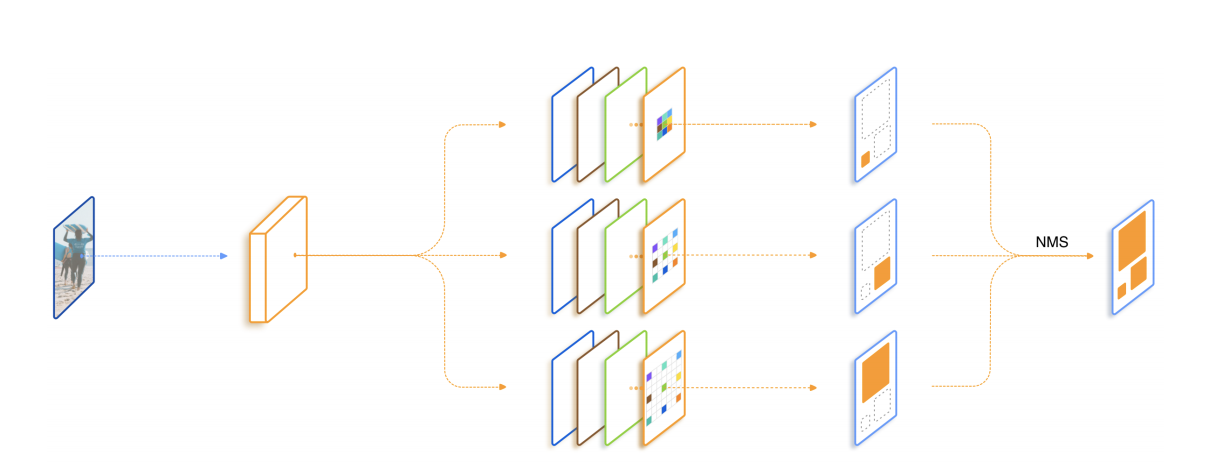
（6） TridentNet：提出了一个拥有三个分支的网络结构， 3个不同的分支使用了空洞数不同的空洞卷积， 感受野由大到小， 更好的覆盖了多尺度的物体分布。 三个分支检测的内容是相同的， 要学习的特征也相同， 不过是形成不同的感受野来检测不同尺度的物体， 借鉴了 SNIP 的思想， 每一个分支只训练一定范围内的样本。

2. 拥挤和遮挡物体检测

(1) 改进 nms： 由于 nms 对遮挡检测影响较大， 因此改进 nms 是一个思路。 比如使用 soft nms 和 IoU-Net 等方法都能在一定程度上提升检测的性能。

(2) 增加语义信息： 遮挡会造成部分信息的缺失， 因此可以尝试引入额外的特征， 如分割信息、梯度和边缘信息等。如 CVPR 2017 的论文 HyperLearner。

(3) 划分多个 part 处理：比如行人之间的形状较为类似， 因此可以利用这个先验信息， 将行人按照不同部位， 如头部、上身、手臂等划分为多个 part 进行单独处理， 然后再综合考虑。

(4) repulsion los: CVPR 2018 的 Repulsion Loss 方法从损失函数的角度出发， 引入了新颖的排斥损失。

(5) OR-CNN: ECCV 2018 的 ORCNN 设计引入了一种新的损失 Aggregation Loss， 使得多个匹配到同一物体标签的 anchor 尽量地靠近； 在 RoI pooling 处根据行人部位分为了 5 个不同的模块， 提出了 PORoI Pooling 方法。

3. 高效 detection

• 可以从模型压缩和加速的角度进行考虑：使用轻量级网络、剪枝、量化、蒸馏等方法对主干网络进行简化。

• 可以从检测框架的角度进行考虑：通过合理的设计 backbone、FPN、head 甚至是重新设计网络结构。

4. 样本不均衡的问题

很多问题， 应该从三个方向进行考虑： 模型(model + loss + nms)、数据、算法

• 一个很直观的方向：修改损失函数， 比如 focal loss 和 OHGM
• 从数据集的角度进行分析：进行数据的重采样、数据的增强、cutmix 操作等

5. 其他的几个问题

• 物体不均衡的问题 & 长尾问题
• 重新思考 nms 和 anchor
• 物体的关系： relation network
• nas
• 实际场景结合：
  • 传感器融合
  • 实际场景的检测：雾霾、雨天、夜晚
• 其他