leetcode-review
1. CPP 语法快速回顾
(1) 声明
// 二维数组的申请
int m, n;
vector<vector<int> > dp(m, vector<int>(n, 0));
// 堆的声明
priority_queue<int, vector<int>, greater<int> > min_heap; // 最小堆
priority_queue<int, vector<int>, less<int> > max_heap; // 最大堆(2) 常见算法
// 常见的算法:
sort、swap、max_element、find、reverse、accumulate、
// 字符串函数
islower(char c) // 是否为小写字母
isupper(char c) // 是否为大写字母
isdigit(char c) // 是否为数字
isalpha(char c) // 是否为字母
isalnum(char c) // 是否为字母或者数字
toupper(char c) // 字母小转大
tolower(char c) // 字母大转小
find_first_not_of //
find_last_not_of //
substr //
// find ---- 返回值为迭代器
// set、map: 自带 find 函数 c.find(val);
// 普通容器 find(c.begin(), c.end(), val);(3) 容器
// begin() end() empty() size()
// stack: 栈 push pop top
// queue: 队列 push pop front
// deque: 双端队列 push_back、push_front、pop_back、pop_front、front、back
// priority_queue: 堆 top、 push、 pop
// vector: 可变数组 pop_back、push_back()、back
// list: 双向链表 func?
// set: s.insert(key_value) erase(key_value) erase(iterator)
// map、unordered_map: m[key] = val; erase(key_value) erase(iterator) 2. 常见的命名:
// 数组
begin、end
left、right
start、end
min_xxx、max_xxx
res、nums
// 堆、栈、队列
m_queue、m_stk、m_deque、max_heap/min_heap、arr
// 关于链表
node、pNode、ptr、p、l1、l2
prev、cur、next、head、tail
dummy
// 二叉树
root、left、right
// 图
matrix、board、grid
i, j, k、m、n、row、col
path
// 哈希表
hash_map、key、val
// 排序、查找、计数
search、find、sort、target、cnt、s、sum、freq
// 递归、回溯、贪心、动规
track、backtrack、dp
// 其他:
reverse、partition、range、
cache、cand、point、amount、rest、flag、base、coins
prime、fill、cap、delete_node、3. 高频题目
括号生成 🌟
(1) 主函数一般是声明 res, track, 调用, 返回 (2)递归函数:不符合返回, 符合处理, 递归调用
搜索旋转排序数组 🌟
先和左端点进行比较(>=)、判定区间是否有序, 然后判断 target 是否在有序区间内 !
接雨水 🌟
max_element 函数
全排列 II 🌟
跳跃游戏 🌟
先判断,再跳跃
合并区间 🌟
根据区间右端点进行排序, 利用 vector, 需要判定是否进行区间覆盖
单词搜索 🌟
-
// 将其转化为接雨水的问题 while(!m_stk.empty() && heights[i] < heights[m_stk.top()]){ int h = heights[m_stk.top()]; m_stk.pop(); int w = m_stk.empty() ? i : i - m_stk.top() - 1; area = max(area, w * h); } 二叉树的层序遍历 🌟
在循环外取 size, 然后进行遍历 需要判断左右子树是否为空
-
(1)前序全局、中序取 map (2)三个参数: pre_root: 根节点在前序遍历中的下标、中序遍历的左侧边界和右侧边界
(3)右子树的根节点: 前序遍历的根节点的坐标 + 左子树的个数 + 1
(4)递归退出条件:if(right < left) return NULL; 二叉树中的最大路径和 🌟
递归处理的几个步骤:何时跳出递归? 处理部分? 递归部分 ? 返回值
helper 函数的作用: 求从根节点出发的最大路径!复制带随机指针的链表 🌟
(1) 一个 node 的 vec、一个 node 2 idx 的 map (2) 别忘记 push_back(0)环形链表 II 🌟
(1) 会证明吗? (2)fast、slow 初始化均为 head, 然后先移动,后判定是否相等二叉树的前序遍历 🌟
前序遍历和中序遍历的区别在 push_back 的位置寻找旋转排序数组中的最小值 🌟🌟
和右端点进行比较, 如果大于 left = mid + 1; 如果小于 right = mid; 如果等于 right—;回文链表 🌟
(1) 求中间值, 翻转,判断回文 (2) 将中间节点的前置节点的 next 指针置零 (3) 两个指针均不为空二叉树的最近公共祖先 🌟
if(left && right) return root; return left ? left : right;用最少数量的箭引爆气球 🌟
按照左端点进行排序排序数组 🌟
几个条件不同:while(left != right)、left < right、nums[left] >= pivot(2) return left最小的k个数 🌟
最小的k个数, 用最大堆, 声明时用 less; 最大的k个数, 用最小堆, 声明时用 greater数据流中的中位数 🌟
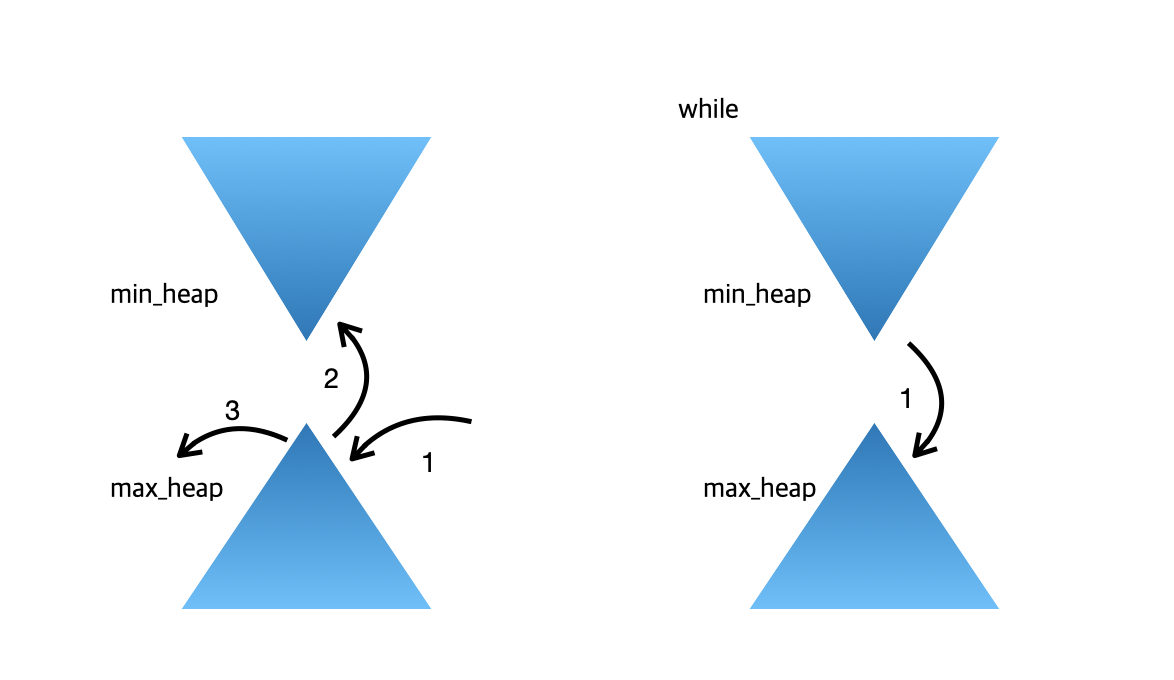
数组中的逆序对 🌟
滑动窗口的最大值 🌟
先进行弹出队列头元素的判断(i - q.front() >= k),再进行添加 (i >= k-1) res 添加的是坐标,而不是元素
LRU 缓存 🌟
以对 cache 的操作为主,对 map 的操作只有满了的时候删除
m_map.erase(cache.back().first)和 两个操作的更改指向m_map[key] = cache.begin()。 其余的基本是对cache 进行操作。BN 操作的实现
def bn_forward(x, gamma, beta, eps): x_mean = np.mean(x, axis=(0, 2, 4), keepdims=true) x_var = np.var(x, axis=(0, 2, 4), keepdims=true) hat_x = (x - x_mean) / np.sqrt(x_var + eps) out_x = gamma * hat_x + beta return out_x-
ListNode* reverse(ListNode * head){ ListNode * prev = NULL; ListNode * cur = head; while(cur){ ListNode * next = cur -> next; cur -> next = prev; prev = cur; cur = next; } return prev; } ListNode* reverseKGroup(ListNode* head, int k) { ListNode * dummy = new ListNode(0); dummy -> next = head; ListNode * prev = dummy; ListNode * tail = dummy; while(tail->next != NULL){ // 首先定位出来 prev 和 tail 节点 for(int i = 0; i < k && tail != NULL; i++) tail = tail -> next; if(tail == NULL) break; // 利用 prev 定位出 start, 利用 tail 定位出 next 节点 ListNode * start = prev -> next; ListNode * next = tail -> next; tail -> next = NULL; // 注意这一句 // 翻转,然后连接链表 prev -> next = reverse(start); start -> next = next; // 更新 prev 和 tail 节点 prev = start; tail = start; } return dummy -> next; }
nms 实现
最核心的几个操作: 解析出来 x1,y1,x2, y2, scores 和 求 iou
排序:order = scores.argsort()[::-1]对 iou 的选择:
iou = ... ids = order[iou < thresh][0] order = order[ids + 1]
4. 参考资料
- https://leetcode.com/
- 《剑指 offer》
- 《Cracking the Coding Interview: 150 Programming Interview Questions and Solutions》
- https://cspiration.com/leetcodeClassification
- https://greyireland.gitbook.io/algorithm-pattern/
- leetcode 刷题班 https://www.bilibili.com/video/BV1GW411Q77S
- https://greyireland.gitbook.io/algorithm-pattern/
- https://github.com/donnemartin/interactive-coding-challenges
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!