一. 数据预处理

1. 中心化

中心化是预处理最常用的形式。它对数据中每个独立特征减去平均值，从几何上可以理解为在每个维度上都将数据云的中心都迁移到原点。在numpy中，该操作可以通过代码X -= np.mean(X, axis=0)实现。而对于图像，更常用的是对所有像素都减去一个值，可以用X -= np.mean(X)实现，也可以在3个颜色通道上分别操作。

2. 归一化

归一化是指将数据的所有维度都归一化，使其数值范围都近似相等。有两种常用方法可以实现归一化。

第一种是先对数据做零中心化（zero-centered）处理，然后每个维度都除以其标准差，实现代码为X /= np.std(X, axis=0)。

第二种方法是对每个维度都做归一化，使得每个维度的最大和最小值是1和-1。

这个预处理操作只有在确信不同的输入特征有不同的数值范围（或计量单位）时才有意义，但要注意预处理操作的重要性几乎等同于学习算法本身。在图像处理中，由于像素的数值范围几乎是一致的（都在0-255之间），所以进行这个额外的预处理步骤并不是很必要。

二. 激活函数

1. 常见的激活函数及其导数

Sigmoid 激活函数的形式为 $f(z) = \frac{1}{1+e^{-z}}$, 对应的导函数为 $f’(z) = f(z)(1-f(z))$

Tanh激活函数的形式为 $f(z) = \frac{e^{z} - e^{-z}}{e^{z}+e^{-z}}$, 对应的导函数为$f’(z) = 1 - (f(z))^2$

ReLU 激活函数的形式为 $f(z) = max(0, z)$, 对应的导函数为 $f'(z)=\left\{ \begin{aligned} 1, z > 0 \\ 0, z \leq 0 \\ \end{aligned} \right.$

2. 为什么 sigmoid 和 tanh 激活函数会导致梯度消失的现象？

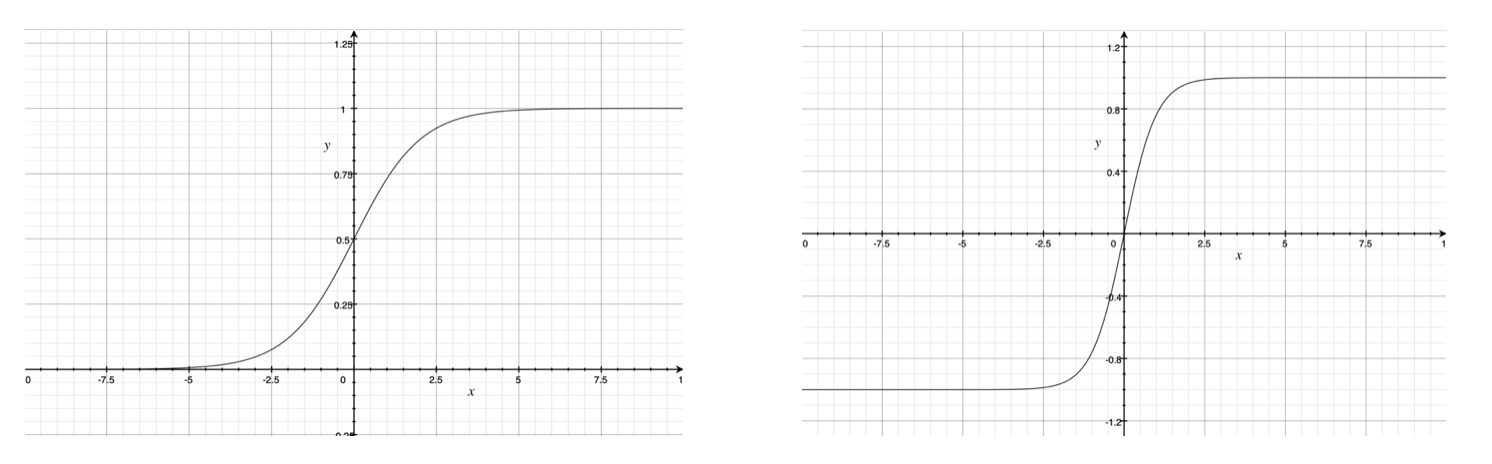
sigmoid 激活函数的曲线如下左图所示。它将输入z 映射到（0, 1），当z很大时， f(z) 趋近于1；当z很小时， f(z) 趋近于0， 而其导函数 $f’(z) = f(z)(1-f(z)) $ 在 z 很大或者很小时都会趋近于0，造成梯度消失的现象。

tanh 激活函数的图像如下右图所示。当z很大时，f(z) 趋近于1， 当z 很小时， z 趋近于-1。 其导数 $f’(z) = 1 - (f(z))^2$ 在 z 很大或很小时都会趋近于0，同样会出现梯度消失。

实际上，Tanh 相当于 Sigmoid的平移： $tanh(z) = 2sigmoid(2x)-1$。

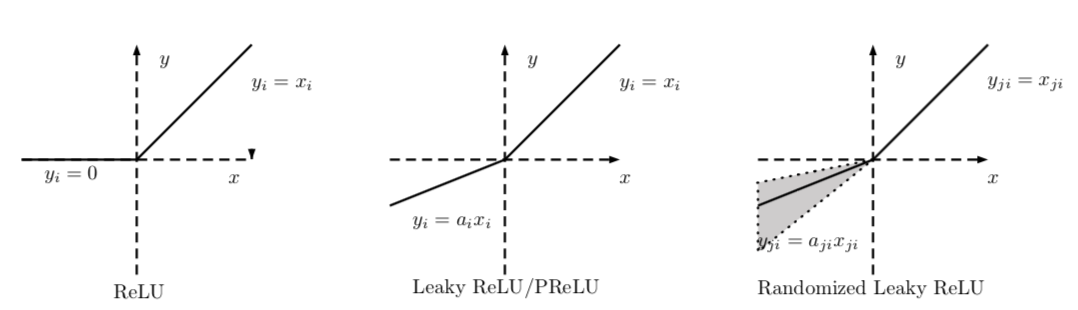
3. ReLU 系列的激活函数相对于 sigmoid 和 tanh 的优点是什么？它们有什么局限性以及如何改进？

优点：

（1）从计算角度上， Sigmoid 和 tanh 激活函数均需要计算指数，复杂度高，而ReLU只需要一个阈值即可得到激活值。

（2）ReLU 的非线性包含线性可以有效地解决梯度消失问题，提供相对较宽的激活边界。

（3）ReLU的单侧抑制提供了网络的稀疏表达能力。

局限性：在训练过程中会会导致神经元死亡的问题。这是由于 $f(z) = max(0, z)$ 导致负梯度在经过该ReLU 单元时被置为0， 且在之后也不被任何数据激活，即流经该神经元的梯度永远为0， 不对任何数据产生响应。在实际训练中，如果学习率设置较大，会导致超过一定比例的神经元不可逆死亡，进而参数梯度无法更新，整个训练过程失败。

一些ReLU 的改进措施：

（1）Leaky ReLU（LReLU）

Leaky ReLU 的表示形式为：$f(z)=\left\{ \begin{aligned} z, z > 0 \\ \alpha z, z \leq 0 \\ \end{aligned} \right.$ ， Leaky ReLU 与 ReLU 的区别在于当 $z\le 0$ 时， 其值不为零，一般来说a 为一个很小的常数(0.01或者0.001数量级的较小整数)，这样既实现了单侧抑制，又保留了部分负梯度信息以致不完全丢失。但另一方面，$ \alpha$ 为超参数，较难设置为合适的值，且较为敏感，因此Leaky ReLU 函数在实际使用中的性能部分十分稳定。

（2）参数化 ReLU（Parametric ReLU，PReLU）：PReLU将负轴部分斜率$ \alpha$ 作为网络中的一个可学习的参数融入模型的整体训练过程。有几点有趣的现象需要注意：

• 自由度较大的各通道独享参数的参数化ReLU性能相比较各通道共享参数更优。

• 在独享参数设定下学到的$ \alpha$取值呈现出由浅层到深层依次递减的趋势，这说明实际上网络所需要的非线性随着网络层数的增加而递减。

  在分类精度上， 使用PReLU 作为激活函数的网络要优于原始ReLU的网络。但是PReLU在带来更大自由度的同时，也增加了网络模型过拟合的奉献，在实际使用中需要格外注意。

（3）随机化ReLU(Random ReLU, RReLU）：增加了“随机化机制， 其取值在训练阶段服从均匀分布，在测试阶段则将其指定为该均匀分布对应的数学期望 $ \frac{l+u}{2}\ $。

（4）指数化线性单元（Exponential Linear Unit， ELU）：2016年 Clevert 等人提出了指数化线性单元 ELU，其公式为： $ELU(x)=\left\{ \begin{aligned} x, x \ge 0 \\ \lambda \cdot (e^x - 1), z \lt 0 \\ \end{aligned} \right.$。ReLU 具备了 ReLU 函数的优点，同时也解决了ReLU 函数自身的“死区”问题。不过ELU 函数中的指数操作稍稍增大了计算量。在实际应用中，ELU 中的超参数 $\lambda$ 一般被设置为1。

三. 网络参数初始化

网络参数初始化方式主要分为四种：

（1）全零初始化：全零初始化会导致网络不通神经元的输出相同，相同的输出导致梯度更新完全一样，这样便会令更新后的参数仍然保持一样的状态，从而无法对模型进行训练。

（2）随机初始化：将参数值随机设定为接近0的一个很小的随机数（有正有负）。

高斯分布：

# origin method
w = 0.001 * randn(n_in, n_out)
# Xavier method 
w = (0.001 * randn(n_in, n_out)) / sqrt(n)
# He method
w = (0.001 * randn(n_in, n_out)) / sqrt(n/2)
# 其中n=n_in或n=(n_in+n_out)/2

均匀分布：

#  Xavier method
low = -sqrt(3/n)
high = sqrt(3/n)
rand_param = low + (high - low) * rand(n_in, n_out)
w = 0.001 * rand_param 
# He mothod
low = -sqrt(6/n)
high = sqrt(6/n)
rand_param = low + (high - low) * rand(n_in, n_out)
w = 0.001 * rand_param

（3）预训练模型初始化

（4） 数据敏感的参数初始化方式 github address

总结：

• 网络参数初始化的优劣在极大程度上决定了网络的最终性能。
• 比较推荐的网络初始化方式为He方式，将参数初始化为服从高斯部分或者均匀分布的较小随机数，同时对参数方差需要加以规范化。
• 另外借助预训练模型中的参数作为新任务的参数初始化方式一种简便异性且十分有效的模型参数初始化方法。

xavier 参数初始化方式的由来：

假设s为未经非线性变化的该层网络输出结果，w为该层参数，x为该层的输入数据，则：

$$Var(s) = Var(\sum_i^nw_ix_i) \\ = \sum_i^nVar(w_ix_i) \\ = \sum_i^n[E(w_i)]^2Var(x_i) +[E(x_i)]^2Var(w_i) + Var(x_i)Var(x_i) \\ = \sum_i^nVar(x_i)Var(w_i) \\ = (nVar(w))Var(x) \\$$

为了保证输出数据 Var(s) 和输入数据Var(x)的方差一致，需令 nVar（w） = 1，即 $n \cdot Var(a\omega)=n\cdot a^2 \cdot Var(\omega’) = 1$， 则 $a=\sqrt{(1/n)}$， 其中$\omega’$为方差规范化后的参数。

四. 目标函数

1. 分类任务的目标函数

(1) 交叉熵损失函数/Softmax 损失函数

交叉熵(cross entropy)损失函数又称Softmax 损失函数，是目前卷积神经网络最常用的分类目标函数。其形式为：

$L{cross\ entropy\ loss} = L{softmax\ loss} = -\frac{1}{N}\sum{i=1}^{N}log(\frac{e^{h{yi}}}{\sum{j=1}^{C}e^{h_j}})$

即通过指数化变换使网络输出 $h$ 转换为概率形式。

(2) 合页损失函数

在支持向量机中被广泛使用的合页损失函数（hinge loss）有时也作为目标函数在神经网络模型中使用：

$L{hinge\ loss} = \frac{1}{N}\sum{i=1}^{N}max{(0, 1-h_{yi})}$

合页损失函数的设计理念是：对错误越大的样本施加越严重的惩罚。可是这一损失函数对噪声的抵抗能力较差。另外，一般的分类任务中的交叉熵损失函数的分类效果略优于合页损失函数的分类效果。

(3) 坡道损失函数

坡道损失函数的定义为：

$$L_{ramp\ loss} = L_{hinge\ loss} - \frac{1}{N}\sum_{i=1}^{M}max{(0, s-h{yi})} \\ = \frac{1}{N}\sum_{i=1}^{M}(max{(0, 1-h_{yi})} - max{(0, s-h_{yi})}) \\$$

其中 , $s$ 制定了“截断点”的文职。由于坡道损失函数实际在 $s$ 处“截断” 合页损失函数，因此坡道损失函数也被称为“截断合页损失函数”(truncated hinge loss function)

(4) 大间隔交叉熵损失函数

上面提到的网络输出结果 $h$ 实际上市全连接层参数 $W$ 与该层特征向量 $x_i$的内积， 即 $h=W^Tx_i$。因此传统的交叉熵损失还可以表示为：

$$L_{softmax\ loss} = -\frac{1}{N}\sum_{i=1}^{N}log(\frac{e^{h_{y_i}}}{\sum_{j=1}^{C}e^{h_j}}) \\ = -\frac{1}{N}\sum_{i=1}^{N}log(\frac{e^{W^T_{yi}x_i}}{\sum_{j=1}^{C}e^{W^T_jx_i}}) \\$$

其中， $W_i^T$ 为$W$ 第i列参数值。根据内积的定义，上式可以变换为

$$L_{softmax\ loss} = -\frac{1}{N}\sum_{i=1}^{N}log(\frac{e^{||W_{yi}||||x_i||cos(\theta_{yi})}}{\sum_{j=1}^{C}e^{||W_{j}||||x_i||cos(\theta_j)}})$$

式中的 $\theta_j(0\leq\theta_j \leq \pi)$ 为向量 $W_i^T$ 和 $x_i$的夹角。以二分类为例，对隶属于第一个类别的某样本 $x_i$而言， 为分类正确，传统的交叉熵损失函数需迫使学到的参数满足 $W_1^Tx_i > W_2^Tx_i$, 亦即$||W_1||||x_i|| cos(\theta) > ||W2||||x_i||cos(\theta)$。大间隔交叉熵损失函数为了使特征更加具有分辨能力，则再次基础上要求二者差异更大，即引入 $m$ “拉大”两者差距，这便是“大间隔”名称的由来。$||W_1||||x_i||cos(m\theta_1) \geq ||W2||||x_i||cos(\theta_2) , (0\leq\theta_1\leq\frac{\pi}{m})$。式中 $m$ 为正整数，起到控制间隔大小的作用，$m$ 越大。类间间隔越大，反之亦然。特别地， 当 $m=1$ 时， 大间隔交叉熵损失函数即退化为传统交叉熵损失函数。

综上可得：

$$||W_1||||x_i||cos(\theta_1) \geq ||W_1||||x_i||cos(m\theta_1) \geq ||W2||||x_i||cos(\theta_2) , (0\leq\theta_1\leq\frac{\pi}{m})$$

可以发现，上式不仅满足传统交叉熵损失函数的约束，在确保分类正确的同时增大了不同类别间分类的置信度，这有助于进一步提升特征分辨能力。

大间隔交叉熵损失函数的定义为：

$$L_{large-margin\ softmax\ loss} = -\frac{1}{N}\sum^{1}_{i=1}log(\frac{e^{||W_i||||x_i||\phi(\theta_{y_i})}}{e^{||W_i||||x_i||\phi(\theta_{yi})}+\sum_{j\neq y_i}e^{||W_j||||x_i||\phi(\theta_{j})}})$$

可以发现，上式与$Softmax$ 损失函数的区别仅仅在于第 $i$ 类分类间隔 “拉大”了：由 $cos(\theta{y_i})$ 变为 $\phi(\theta{y_i})$, 其中：

$$\phi(\theta) = \begin{equation} \left\{ \begin{array}{**lr**} cos(m\theta), 0 \leq \theta \leq \frac{\pi}{m}& \\ \mathcal{D}(\theta) , \frac{\pi}{m} < \theta \leq \pi &\\ \end{array} \right. \end{equation}$$

式中，$\mathcal{D}(\theta)$ 只需要满足“单调递减”条件， 且 $D(\frac{\pi}{m})=cos\frac{\pi}{m})$。

(5) 中心损失函数

大交叉熵损失函数主要考虑增大类间距离，而中心损失函数则在考虑类间距离的同时还将一些注意力放在减小类间差异上。中心损失函数的定义为：

$$L_{center\ loss} = \frac{1}{2}\sum_{i=1}^{N}||x_i - c_{y_i}||_2^2$$

其中， $c_{y_i}$ 为 第 $y_i$ 类所有深度特征均值的中心，故名“中心损失函数”。

在实际使用中，由于中心损失函数本身考虑类内差异，因此应该讲中心损失函数与其他主要考虑类间距离的损失函数配合使用，如交叉熵损失函数，这样网络最终目标形式可表示为：

$$L_{final} = L_{cross\ entropy\ loss} + \lambda L_{center\ loss}(h, y_i) \\ = -\frac{1}{N}\sum_{i=1}^{N}log(\frac{e_{h_{y_i}}}{\sum_{j=1}^{C}e^{h_j}})+\frac{\lambda}{2}\sum_{i=1}^{N}||x_i - c_{y_i}||_2^2$$

2. 回归任务的目标函数

(1) $\mathcal{L1}$ 损失函数

$$L_{\mathcal{l1}} = \frac{1}{N}\sum_{i=1}^{N}\sum_{t=1}^{M}||y_t^i-\hat{y}t^i||$$

(2) $\mathcal{L2}$ 损失函数

$$L_{\mathcal{l2}} = \frac{1}{N}\sum_{i=1}^{N}\sum_{t=1}^{M}(||y_t^i-\hat{y}t^i||)^2$$

在实际使用中， $\mathcal{l_1}$ 与 $\mathcal{l_2}$ 损失函数在回归精度上几乎相差无几。不过在一些情况先 $\mathcal{l_2}$ 损失函数会略优于 $\mathcal{l_1}$ ，同时收敛速度方面 $l_2$ 损失函数也略快于 $\mathcal{l_1}$ 损失函数。

(3) Tukey’s biweight 损失函数

Tukey’s biweight 损失函数是一类非凸函数，其可克服在回归任务中的利群店或者样本噪声对整体回归模型的干扰和影响，是回归任务中一种健壮的损失函数，其定义如下：

$$\mathcal{L_{Tukey's\ biweight\ loss}} = \begin{equation} \left\{ \begin{array}{**lr**} \frac{c^2}{6N}\sum_{i=1}^{N}\sum_{t=1}^{M}[1-(1-(\frac{l_t^i}{c})^2)], |l_t^i| \leq c \\ \frac{c^2{M}}{6}, 其他 &\\ \end{array} \right. \end{equation}$$

式中， 常数 $c$ 指定了函数拐点的位置。需要说明的是，该超参数并不需要认为指定。一般情况下， 当 $c=4.6851$ 时， $Tukey’s\ biweight $损失函数可取得与 $\mathcal{l_2}$ 损失函数在最小化符合标准正态分布时的残差类似的(95%渐进)回归效果。

3. 其他任务的损失函数

在一些如人脸年龄估计、头部角度识别等任务样本标记具有不确定性的特殊场景下，基于标记分布(label distribution)的损失函数不失为一种优质的选择。具体而言，假设 $h=(h_1, h_2, …, h_C)^T$ 为模型对于输入样本 $x_i$ 的最终输出结果，那么在利用标记分布技术解决问题之前，首先需要将 $h$ 转化为一个合法分布。以softmax 为例可以将 $h$ 转化为:

$$\hat{y}_k = \frac{e^{h_k}}{\sum_{j=1}^{C}{e^{h_j}}}$$

其中，$k \in {1,2,3,…,C}$ 代表标记向量的第 $k$ 维。

可以用Kullback-Leibler散度(KL divergence)来度量 $\hat{y}$与真实标记 $y$ 之间的误差：$\mathcal{L}_{KL\ loss}=\sum_k{y_klog\frac{y_k}{\hat{y}_k}}$。

由于 $yk$ 为常量，上式等价于：$\mathcal{L}{KL\ loss} = -\sum_{k}{y_k}{log{\hat{y}_k}}$。通过该式可以衡量样本标记分布与真实部分之间的差异，并利用该差异指导模型训练。